X-photon 3D lithography by fs-oscillators: wavelength-independent and photoinitiator-free

The versatility of the non-photosensitized SZ2080^TM, is firstly demonstrated by manufacturing 3D woodpiles, using laser oscillators with all three available different wavelengths: 517, 780 and 1035 nm. As SZ2080^TM, with or without PI, is transparent to all the employed laser wavelengths, the nonlinear absorption is required to induce photopolymerization. To spectrally match the absorption corresponding to linear 259–260 nm absorption, the 517 nm needs 2-photons, the 780 nm 3-photons, and the 1035 nm proportionally 4-photons to be simultaneously absorbed. This is also corresponding to the required photon energy to cause the excitation⁵⁴. In particular, the effectiveness of the different laser oscillators for inducing MPL the non-photosensitized SZ2080^TM, is proven experimentally by fabrication of the well-defined 3D woodpiles, with dimensions 20 × 20 × 15 µm³ and in-layer periodicity of 1 µm as presented in Fig. 1.

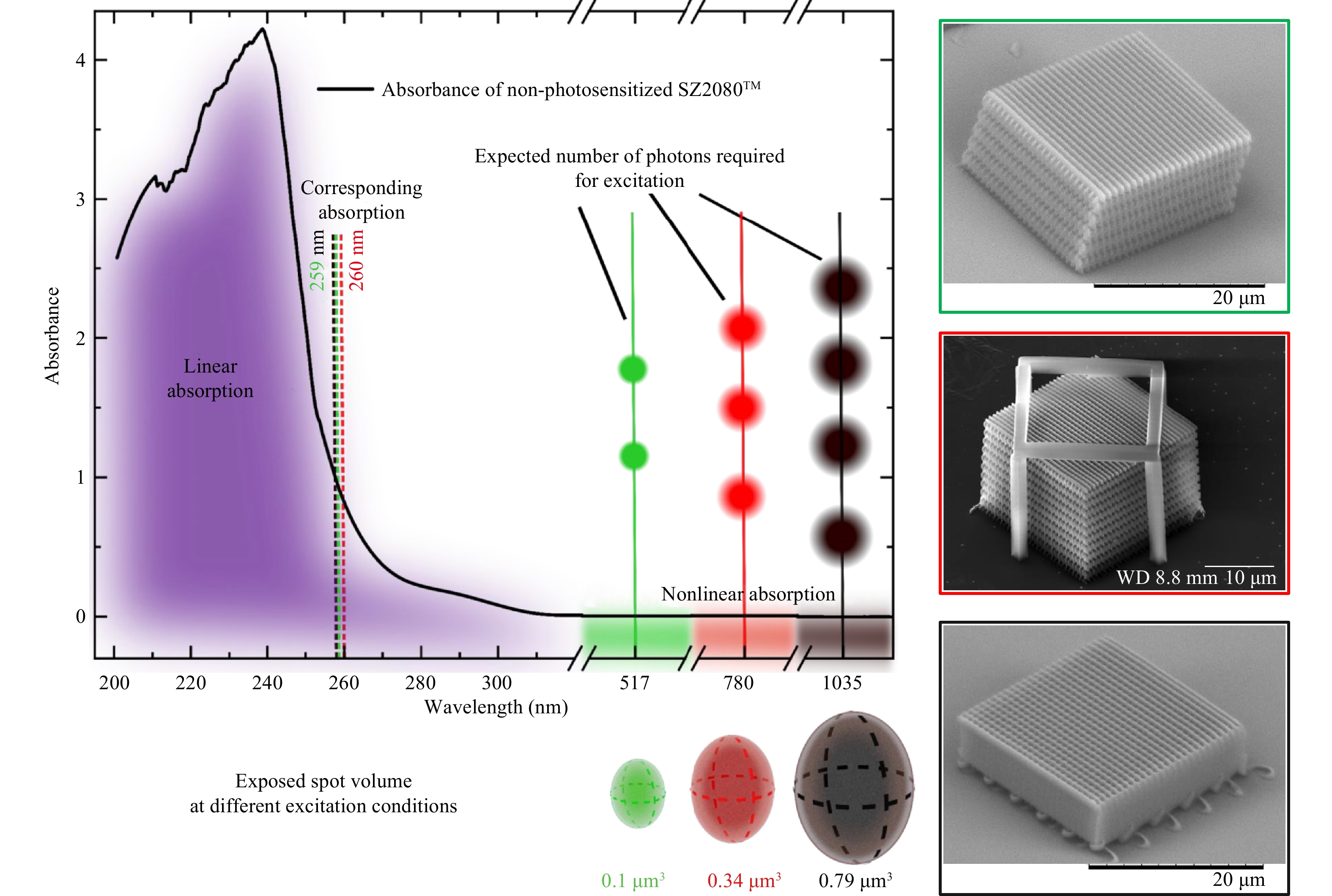
Fig. 1  Absorbance spectrum of the non-photosensitized SZ2080^TM with the estimated exposed spot volumes under 1.4 NA focusing conditions (refer to table S1 for calculations) for the three different laser excitation wavelengths. On the right: 3D woodpile structures fabricated with corresponding 517 nm (green), 780 nm (red) and 1035 nm (black) laser sources. Note that all three wavelengths are multiples of the 259–260 nm were absorption is expected for 2, 3 and 4 photon absorption to happen. The absorption spectrum of baked SZ2080^TM has been adapted from the thin film measured previously¹, without directly assessing its thickness but being orders of magnitude higher than the incident light wavelength. A strong absorbance is defined $ OD > 1 $, where $ Absorbance\equiv OD = -\lg T $ with $ T=10^{-OD} $ (see dashed lines for spectral position of the Multi-Photon Absorption (MPA) at $ OD\sim 1 $).

Next, the materials composition influence on the processing of the non-photosensitized SZ2080^TM and its derivatives at 780 nm laser excitation are presented. By varying the concentration of its organic component, the process window is obtained for each molar concentration of ZPO:MAA (Fig. 2a). It is compared with the process window of the photosensitized SZ2080^TM with a molar concentration of ZPO: MAA = 1:1 and 1% w/w, in respect to the monomers concentration of Michler’s ketone as PI. In order to quantify the process windows of the photoresists, 3D cubes with dimensions of 20 × 20 × 5 µm³ were fabricated using a galvo-scanner at a scanning speed of 5 µm/s uder focusing with 40x/0.95 NA objective lens. The laser power was varied from 75–200 mW (at a repetition rate of 80 MHz) corresponding to an average pulse intensity of I = 0.58–1.55 TW/cm² (refer to table S1 for details on calculating I). An example of the polymerized cubes is shown in the Fig. S5. The increase in the organic component within the non-photosensitized SZ2080^TM results in DFWs narrowing from half to quarter of the photo-sensitized one's, shown in Fig. 2b. In all cases, it was still possible to fabricate structures by adjusting the exposure parameters. This somewhat matches with the comparison of various PIs with increased efficiency, which widens the DFWs in respect to common ones⁵⁵. Namely, the polymerization threshold (i.e., light green color in Fig. 2a, which is defined as the minimum intensity where a 3D cube is formed and survives the development, remains almost stable for all non-photosensitized resist compositions (see Fig. S4 for the details of the results). The burning/damage threshold, defined as the maximum intensity that a deformed/burned cube is observed after the development, is higher for the ZPO: MAA = 1:1 (~1.35 TW/cm²) compared to ZPO: MAA= 1:3 and 1:4 (~1.08 TW/cm²). These observations can be attributed to the increased absorption due to the higher concentration of the organic component and that it requires less energy for polymerization reaction (more available carbon double bonds for cross-linking), as well as lower optical breakdown threshold^{37, 51}. Consequently, enhanced cross-linking occurs in shorter times. However, as polymerization reaction is exothermic, the higher concentration of the organic component results in burned structures. This may also be due to the typically lower resilience of organic substances. The DFW is presented for the different molar concentrations of ZPO:MAA in Fig. 2b. DFW is obtained by the equation shown in Fig. 2b, using the polymerisation and burning / damage threshold values of the process window. The DFW shrinks when the concentration of the organic component of the non-photosensitized SZ2080^TM increases (see later Sec. Discussion 2 for the mechanisms of energy deposition).

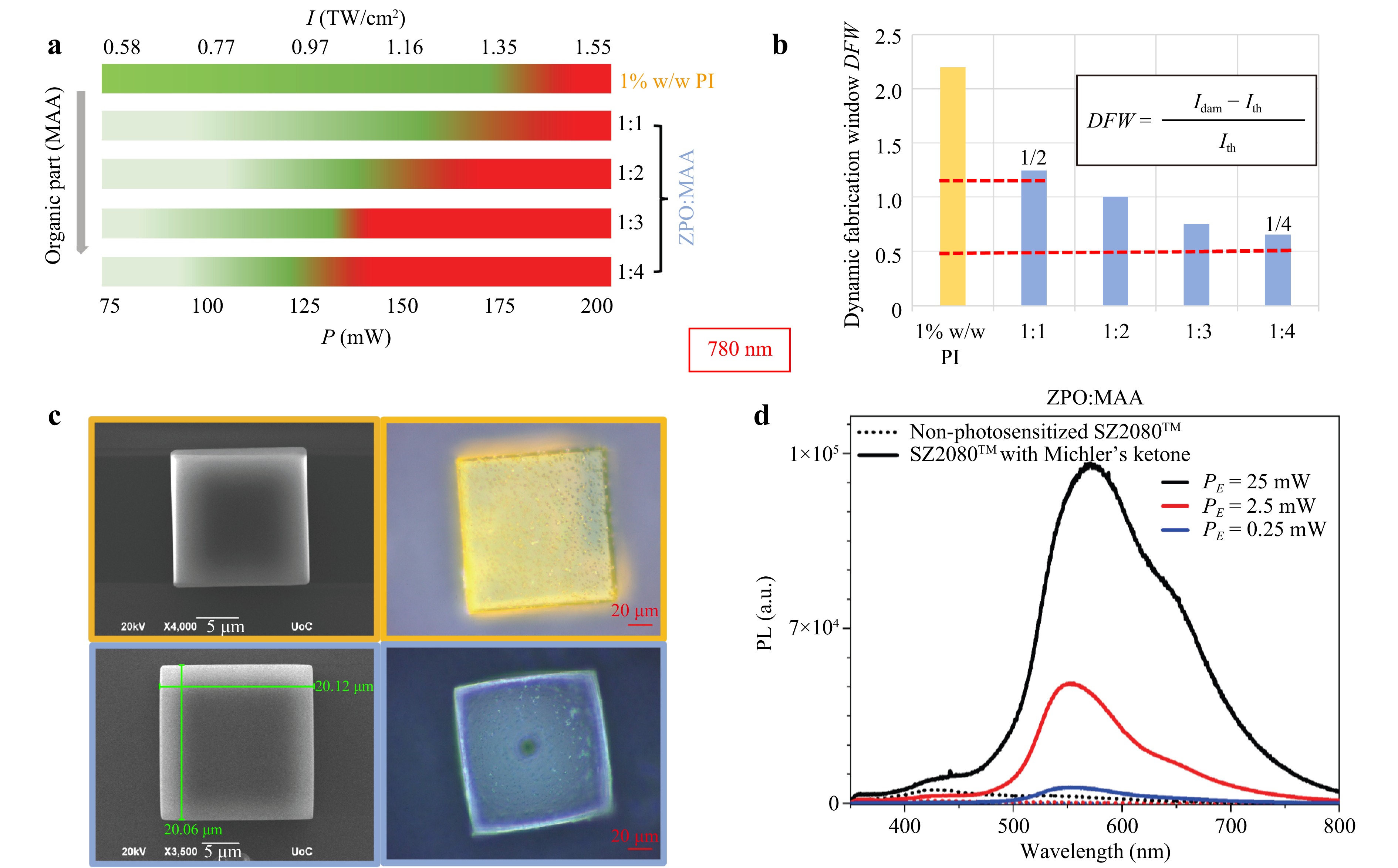
Fig. 2  a Processing window of the of the SZ2080^TM with 1% w/w Michler’s ketone as PI and compared to non-photosensitized SZ2080^TM compositions consisting of different concentrations of the organic parts. Green - repeatable fabrication, red and white - burning or collapsing structures, respectively. b The dynamic fabrication window (DFW) in relation to the molar concentrations of ZPO:MAA (light-blue) and the DFW of the photosensitized SZ2080^TM (light-yellow). c SEM and fluorescent optical microscope images of 3D cubes. The yellow frame is for the 3D micro-cubes fabricated with photosensitized SZ2080^TM and the blue one the non-photosensitized SZ2080^TM. Polarisation of fs-laser writing was linear (along the scan direction). d Photoluminescence measurements of the photosensitized SZ2080^TM (solid lines) and the non- photosensitized SZ2080^TM (dashed line), excited with P_E = 0.25 mW (blue), 2.5 mW (red) and 25 mW (black) at wavelength of 325 nm CW irradiation.

A demonstration of a fabricated 3D cube of the non-photosensitized SZ2080^TM by utilizing an 780 nm laser source is presented in Fig. 2c (bottom) and compared with a 3D cube of the photosensitized SZ2080^TM(top). On the right of Fig. 2c, fluorescence microscope images are shown of the 3D cubes, indicating a significantly lower fluorescence of the 3D cube fabricated with the non-photosensitized SZ2080^TM compared to the photosensitized one. This indication is proved experimentally by micro-photoluminescence measurements. Specifically, in Fig. 2d, the fluorescence of the photosensitized SZ2080^TM is shown to be one order of magnitude higher than the non-photosensitized one, for all the excitation powers applied on the 3D cubes. Thus, the presence of the PI contributes tremendously to the fluorescence intensity of the structures, while its absence results to almost zero fluorescence. Additionally, the fluorescence spectrum of the non-photosensitized SZ2080^TM can be attributed to the rest of the material's components.

A parametric study was conducted for the fabrication parameters of the 3D woodpiles employing the three different wavelengths of laser oscillators, demonstrated in Fig. 3. Firstly, 3D woodpiles were fabricated using the 517 nm laser oscillator. The intensity I at the focus during the fabrication of the 3D woodpiles was in the range of 0.27–4.07 TW/cm² for all the structures shown in Fig. 3a while the scanning speed was varied from 30–10⁵ µm/s. On the other hand, the scanning speed during the fabrication of the 3D woodpiles employed by the 780 nm laser oscillator using the Nano setup shown in Fig. 3b (detailed later in Materials and Methods section), was kept constant at 30 µm/s, while the intensity at the focus I was varied from 0.96 to 1.18 TW/cm². It is important to mention here that the intensities used for the fabrication of the 3D woodpiles are similar to the ones used for the cubes. However, this does not mean that the thresholds of cubes and woodpiles are the same, as they are two different geometries requiring different scanning density/exposure overlap contributing to the accumulated delivered energy density. However, in Fig. 3b, it is proved again that the fabrication window of the non-photosensitized material is narrower. Specifically, as the intensity at the focus during fabrication is higher the 3D woodpiles are deformed, similarly with the 3D cubes fabrication. Additionally, in the case of the fabrication of the 3D woodpiles using the 780 nm laser source, the printing process was more sensitive. As a result, in some cases, the woodpiles disappeared during the development process because they did not adhere well to the substrate. To address this, we added frame support to make the structures more stable In Fig. 3c the fabrication highlights of the non- photosensitized SZ2080^TM utilising the three laser wavelengths is illustrated. Specifically, in red frame is shown the higher resolution (smallest feature dimensions) that was achieved with the 780 nm laser source, which was 277 nm line-width, similar resolution (130−500 nm) that has been reported for photosensitized materials used in MPL²⁸. The proof of concept for wavelength-independent structuring of non-photosensitized SZ2080^TM is illustrated in Fig. 3 with black frame, where 3D woodpiles were fabricated using the 1035 nm laser oscillator, resulting in well-defined structures. In addition, manufacturing of large-scale 3D woodpiles with high scanning speed, using the 517 nm laser source, is demonstrated in green frame. In terms of speed and object dimensions it is comparable with the photo-sensitized SZ2080^TM using amplified laser pulses of the same wavelengths, reported previously⁵⁶, therefore proving that it is still possible to structure this material when removing the PI and switching to non-amplified laser oscillators as excitation sources.

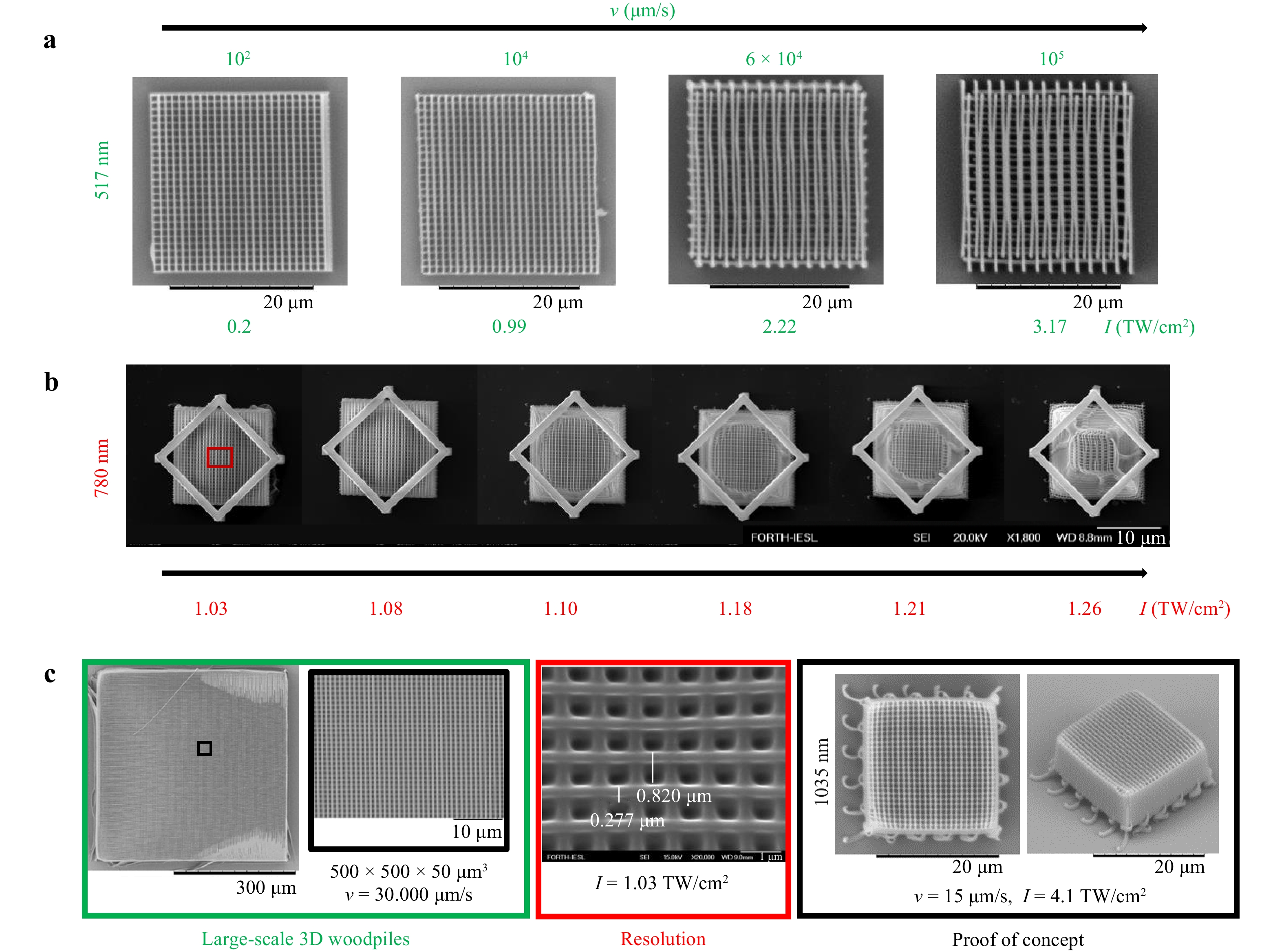
Fig. 3  a 3D woodpiles are shown fabricated using the 517 nm laser source with different scanning velocities and intensities. b 3D woodpiles developed with the 780 nm laser source with a scanning speed at 30 µm/s while the power is altered from 20.5–25 mW. c The fabrication highlights of the non-photosensitized SZ2080^TM are presented for 1035 nm (black frame), 780 nm (red frame) and 517 nm (green frame).

An interesting experimental observation of the 3D photo-polymerisation of photoinitiator-free and wavelength independent character presented above needs better understanding. Obviously, the energy deposition channel into focal volume holds the answer. The light-matter interaction is dependent on the permittivity $ \varepsilon\equiv \tilde{n}^2 $ of material, where the refractive index $ \tilde{n} \equiv n+i\kappa $ has real and imaginary parts $ n,\kappa $, respectively and $ i\equiv\sqrt{-1} $. Permittivity defines the portions of reflected and absorbed (deposited) light intensity. Optical nonlinearities where energy deposition is instantaneously affected by a different order of intensity $ I^X $, where $ X $ is the scaling exponent dependent on the order of multi-photon, or avalanche, or saturable character of absorption. This spatio-selectively photo-deposited energy leads to the final cross-linking via thermal, chemical, and structural changes over a wide temporal range, from picoseconds to femtoseconds. Next, we estimate the energy deposition at the threshold conditions of MPL 3D printing.

Energy deposition per volume [J/cm³] is the key parameter for heating, chemical bond breaking, radical generation for cross-linking, and free electron generation⁵⁷. The instantaneous value of the permittivity of material $ \varepsilon $ at the focal volume determines direct energy deposition (more detailed explanation in equations can be found in Ref. 6, Section 2.3 on Energetics of laser 3D polymerization). The permittivity is the square of the complex refractive index $ \varepsilon = (n^2-\kappa^2) + i2n\kappa $ and defines portions of the reflected $ R $ and absorbed $ A $ parts of light, hence, transmitted $ T $ as well as guided by the energy conservation $ A+R+T=1 $. Once free carriers (electrons) are generated by MPA, $ n $ is decreasing while $ \kappa $ is increasing. This process is ultimately driven to dielectric breakdown via positive feedback loop; the dielectric breakdown is defined as the real part of permittivity equals to zero: $ n^2-\kappa^2 $ = 0. The range of real part of permittivity between 1 and 0 is called epsilon-near-zero (ENZ) state which has strong absorption. We analyse energy density [J/cm³] required for polymerization threshold. Loss of structural integrity of 3D pattern can be linked to the dielectric breakdown, hence, $ n=\kappa $. The ENZ conditions would be created first at the very center of the focal spot (peak of intensity) as was observed in structural damage of dielectrics including silica glass⁵⁸. Counter intuitively, this localisation of energy deposition takes place into the region of the reduced $ n $ (due to photo-ionisation), where, simultaneously, $ \kappa $ is increased, hence, also the absorption coefficient $ \alpha = 4\pi\kappa/\lambda $ is augmented. This is caused by the requirement of the normal components of the displacement $ D = \varepsilon E $ being continuous across the interface of the larger-smaller refractive index $ n $. Previously this phenomenon was used to nano-ablate grooves on thin films⁵⁹. Importantly, this energy localisation is only effective when it is at the interface and on a scale of tens-of-nm within the region large-smaller-larger $ n $ (as between two plasmonic nanoparticles). This is the primary cause of sub-diffraction-limited laser ablation in 2D⁵⁹ and 3D⁵⁸. The nanoscale localisation of intensity on the side of interface where the refractive index is lower $ n_{low} $ (tip of intensity) as compared to surrounding unperturbed resist $ n_0 $ is $ I_{low}\equiv E_{low}^2 = \left({n_0}/{n_{low}}\right)^4 I_0 $; since $ \varepsilon\propto n^2 $. Strong intensity enhancement due to this fourth-order scaling is expected, hence, energy deposition as well (also helped by the augmented $ \kappa $ at the same region where $ n_{low} $ is reduced). Noteworthy, this scaling of energy deposition has origin from the boundary conditions rather the absorption mechanism which is responsible for the free carriers generation (via photo-ionisation) at the intensity maximum. Qualitatively, the width of polymerized resolution bridges at different wavelengths (very different focal volumes) is consistent with the above-described nano-scale localisation of energy deposition at the very tip of intensity profile, hence, wavelength-independent. Naturally, sub-diffraction limited resolution is readily achievable with this ENZ localisation of energy deposition. This phenomenon is defined by photo-ionisation of the polymer matrix, hence, is not dependent on photoinitiator which has resonant wavelength for absorption by PI molecules which have ~1% wt fraction. The absorption into $ n_{low} $ region is independent on PI and takes place into the photo-ionised pure host material (i.e., 100% wt).

Thermal accumulation due to tens-of-MHz repetition rate is another contributing factor to overall energy deposition. Let us make some estimations for typical pulse intensities and different wavelengths for selected low scan speeds used in experiments $ v_{sc}^{\lambda} $ conditions when heat accumulation is the strongest, namely $ v_{sc}^{517,780}\approx 30 $ μm/s and $ v_{sc}^{1035}\approx 15 $ μm/s. It was established empirically that a low scanning speed ensured the highest repeatability of 3D polymerisation. Typical intensity conditions for woodpile structuring at aforementioned speeds were: $ I_p^{517} = 0.31 $ TW/cm², $ I_p^{780} = 1.01 $ TW/cm² and $ I_p^{1035} = 2.96 $ TW/cm²; The intensity scaling with photon energy $ h\nu\equiv hc/\lambda $ is matching $ I_p\propto (h\nu)^4 $ (see schematics in Fig. 1). The corresponding energy of a single pulse, with transmission losses accounted at the focal point, was correspondingly $ E_p^{517}\approx 17 $ pJ, $ E_p^{780}\approx 212 $ pJ, $ E_p^{1035}\approx 944 $ pJ (the fluences per pulse $ F_p^{517} = 11 $ mJ/cm², $ F_p^{780} = 58 $ mJ/cm², $ F_p^{1035} = 148 $ mJ/cm². The $ I_p $ and $ F_p $ grow slower compared to $ E_p $ due to the former being normalized to the extended size of the exposed focal area.

The dwell time required for the beam to cross the focal diameter (alternatively, spot size scan time see Fig. 4a,b) $ 2r_{\lambda} $ is $ \tau_{dw}^{\lambda}={2r_{\lambda}}/{v_{sc}^{\lambda}} $ and at the repetition rate $ R $, defines the number of accumulated pulses over the focal spot $ N = \tau_{dw}^{\lambda}R $; the values are: $ \tau_{dw}^{517} = 15\; $ ms ($ N \approx 1.14 \cdot 10^{6} $), $ \tau_{dw}^{780} = 23\; $ ms ($ N \approx 1.72 \cdot 10^{6} $), $ \tau_{dw}^{1035} = 60\; $ ms ($ N \approx 4.57 \cdot 10^{6} $). Thermal spread (cooling) of the laser-heated focal volume is defined by the time $ t_{th}^{\lambda} = (2r_{\lambda})^2/D_T $, specifically for investigated cases $ t_{th}^{517} = 290 $ ns, $ t_{th}^{780} = 660 $ ns, $ t_{th}^{1035} = 1162 $ ns while a time separation between pulses is only $ 1/R = 12.5 $ ns. A low thermal diffusivity of the glass-like resist is assumed for evaluation $ D_T=\chi/(c_p\rho)\approx 7\times 10^{-7} $ [m²/s]⁶⁰ enhance the local temperature rise via accumulation (here $ \chi\approx 1 $ [W·m⁻¹·K⁻¹] is the thermal conductivity, $ \rho\approx 2.2 $ [g/cm⁻³] is the mass density, and $ c_p\approx 700 $ [J/(kg·K)] is heat capacity at constant pressure. This estimate shows that the expected thermal accumulation can be calculated here for spot diameter. It is noteworthy, that actual energy deposition takes place into the volume, which has depth of skin depth. Due to a higher effective intensity at the center of the beam where $ I_{low} $ is formed as discussed previously, the depth of energy deposition defined as the skin depth $ l_{skin}=1/\alpha $ scales with local photo-ionisation via $ \kappa\propto\alpha $ and favors more shallow energy deposition at the very tip of intensity profile. The experimental evidence of such energy accumulation could also be implied from the Fig. 4c. The threshold power $ P_{th} $ corresponds to the degree of 3D cross-linking when structure can withstand capillary forces of development and is defined with the accumulated dose J/cm$ ^3 $. The dwell time is proportional to the number of accumulated pulses $ \tau_{dw}\propto N $. The experimental data show trend $ P_{th}\propto\tau_{dw}^{-0.33} $ (c). This is consistent with the accumulation in the Exposed Volume (EV), which can be defined as $ P_{th}(N) = P_{th}(1)\times N^{1-S} $, where the $ P_{th}(N) $ is the threshold power(dose) for $ N $ pulses, $ P_{th}(1) $ is the threshold for one pulse $ N=1 $, and $ S $ is the accumulation exponent; when $ S = 1 $ there is no accumulation. The experimental trend shown in (c) can be fitted with $ S\approx 1.33 $, which shows that there is the accumulation effect $ S>1 $. This is an empirical fact and reflects all processes of heat accumulation, exothermic action of cross-linking, statistics of chemical bond breaking and free radical (polymerizable species) generation within the focal volume. This scaling is applicable over large range of $ \tau_{dw}\sim N $ and could allow to compare different photo-polymerisable materials and writing conditions (wavelength, pulse duration, etc.). For inclusion of scanning speed/exposure duration, we propose to introduce the Dynamic Exposure Volume (DUV), which takes into account the volume which was scanned during certain normalized period of time, thus enabling estimation of surface and volume for energy deposition and diffusion of radical, quenchers, as well as thermal diffusion/cooling.

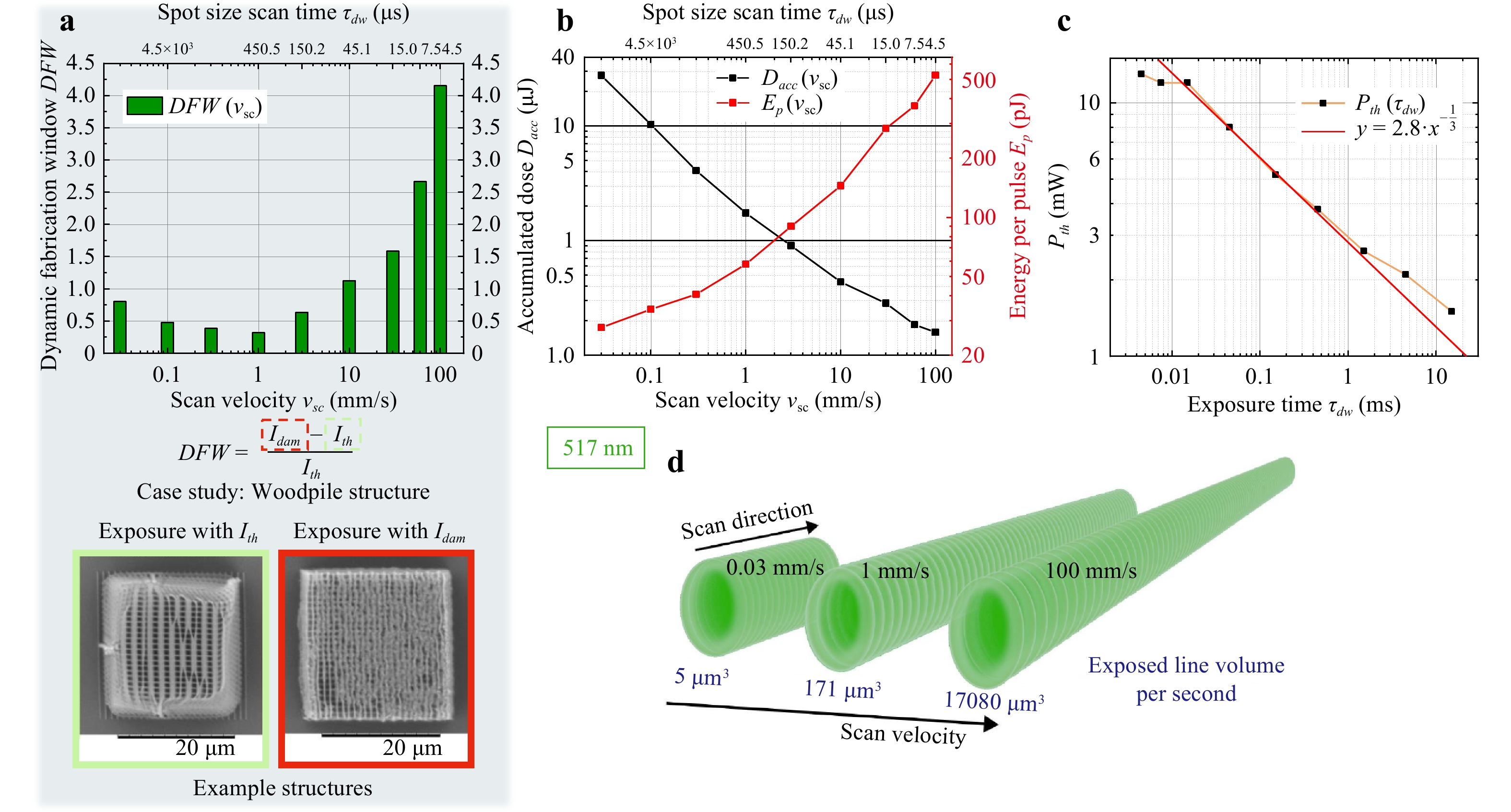
Fig. 4  a Dynamic Fabrication Window (DFW) determined for 25 × 25 × 10 μm³ (design, not accounting for shrinking) woodpile structure (line and layer spacing was set to, respectively 1 μm and 0.66 μm) fabricated employing 517 nm exposure for different scanning velocities ($ v_{sc} $) spanning 4-orders of magnitude, showcasing exemplary samples at DFW extremes: development survivability and damage thresholds. b Average energy which is delivered to the material per spot size scan time $ \tau_{dw} $, i.e accumulated dose $ D_{acc}=P_{avg}\tau_{dw} $ ($ P_{avg} $ - incident power after objective lens) vs different $ v_{sc} $, together with corresponding required pulse energy $ E_{p}={P_{avg}}/{R} $ (not accounting for objective lens losses). c The polymerisation threshold power for retaining design integrity of investigated woodpile structure vs. the dwell (exposure) time $ \tau_{dw} $. The line (in log-log plot) represents a trend $ y\propto x^{-1/3} $, which is consistent with energy-per-volume dose J/cm³, i.e., smaller power requires longer dwell time to accumulate the cross linking dose (see details in the text). d illustrates Dynamic Exposed Volume (DEV), which corresponds of Exposed Volume (EV) translated along the scanning direction proportional to the distance travelled per time unis (1 s) - exposed line volume per second. Varying speed it alters a lot the volume and surface of it dramatically influencing the heat accumulation and dissipation by thermal diffusion.

A strong thermal accumulation is expected at the used LDW conditions with tens-of-MHz repetition rates even at tight focusing and considerably fast beam scan. An average temperature drop at the arrival of the next pulse occurs due to heat transfer to surrounding cold material. The temperature accumulation $ T_N $ can be explicitly calculated for the $ N $ pulses, when single pulse temperature jump is $ T_1 $⁶¹:

where $ \beta = \sqrt{{t_{th}}/({t_{th}+1)/R}} $ is the constant which defines heat accumulation; $ \,\beta\rightarrow 1 $ at high repetition rate $ R\rightarrow \infty $. For the used experimental conditions, $ \,\beta\approx 0.978 $ ($ \lambda = 517 $ nm), $ \,\beta\approx 0.990 $ ($ \lambda = 780 $ nm), $ \,\beta\approx 0.994 $ ($ \lambda = 1035 $ nm). Taking just the first $ N = 10^3 $ pulses, causes significant temperature jump for all exposures $ T_{1000} = 45.6T_1 $ ($ \lambda $ = 517 nm), $ T_{1000} = 101.8T_1 $ ($ \lambda $ = 780 nm), $ T_{1000} = 177.5T_1 $ ($ \lambda $ = 1035 nm). Considering the exothermic character of polymerization, a minute temperature rise at the focal region causes a guided thermal polymerisation⁶².

It was observed that the DFW using PI widens mainly due to lower polymerization threshold but also due to slightly higher damage threshold (1 A). Though it is surprising result it provides insight that the PI is not only enhancing absorption to lower the polymerization threshold, but also takes off some of the energy from the heating via fluorescence and conversion into the chemical means to cause the cross-linking. Such behaviour damps some of the energy overdose, which was noticed similarly using amplified pulses¹⁷.

Finally, once energy deposition reaches conditions of dielectric breakdown $ Re{(\varepsilon)} = n^2-\kappa^2 = 0 $, a runaway plasma breakdown expands the focal region and usually propagates towards the incoming beam. When energy deposited per volume $ w_{en} $ J/cm³ exceeds the mechanical strength of the resist with the Young modulus of few-GPa, then structural damage takes place. Note, the J/cm³ is equivalent to N/cm², the units of pressure. Another important factor for energy deposition has a saturable nature as the photo-excited electronic plasma density $ n_e $ is approaching the critical density (wavelength dependent) $ n_{cr} $ as $ w_{en}\propto({n_e}/{n_{cr}})F_p $⁶³, where $ F_p $ is the fluence per pulse (proportional to intensity). As $ n_{cr} $ is approached with increasing electron plasma generation, the most efficient energy deposition takes place $ {n_e}/{n_{cr}}\rightarrow 1 $, i.e., the ENZ state of the dielectric-to-metal Die-Met phase⁶⁴. The intensity scaling of electron generation $ n_e\propto I_p^X $ defines the mechanism of the process. However, as shown in previous experimental 2D and 3D structuring of transparent materials, an additional enhancement and localisation of energy deposition at nanoscale takes place via ENZ state and boundary conditions at the lowered refractive index region at the very center of intensity envelope. Hence, the “every green” topic of polymerization mechanisms is not so simplistic in terms of intensity exponent, however, can be fully harnessed for the required resolution and throughput. Noteworthy, that a demanding control of energy deposition in time and space is required since the Most Perfect Polymerisation (MPP acronym would coincide to the same MPP like for Multi-Photon Polymerization) is close to the dielectric breakdown and plasma runaway $ n=\kappa $.

Interestingly, the features produced via different exposure wavelengths did not differ significantly in sizes as would be expected to their corresponding exposed volumes (see Fig. 1: the spot sizes are few times and exposed volumes are of magnitude different). More specifically, without a dedicated optimisation study (out of scope of this research paper), the 517 nm wavelength did not allow for producing clearly smaller line-widths in respect to 780 nm or 1035 nm, e.g. typical feature sizes achieved in the aforementioned cases Fig. 3. A, C at low scanning velocity conditions include 314 nm line-width at 1035 nm (2.96 TW/cm²; 15 μm/s) and 345 nm for 517 nm (0.42 TW/cm²; 100 μm/s). The last one of which was even manufactured near the damage threshold conditions (Fig. S6), suggesting that feature size tunability is more pronounced as a function of DFW than the exploited wavelength. These observations are in agreement with our previous study employing amplified laser pulses of 100 – 300 fs pulse-width lower repetition rate of 1 MHz⁴⁰. This indicates that the resulting feature dimensions are of cumulative effect of light-energy delivery and material-properties, rather than just excitation wavelength and optical power. Additionally, it is noted that the polymerization threshold, that means required intensity for the structuring and survival of the structures, is geometry dependent: single dots, suspended lines, porous woodpiles, and bulky lenses / cubes will have different threshold apparently due to different energy deposition. Such dependence was also noted in the report studying the efficiency PIs judging by their DFW values⁵⁵.. This makes the generic term fabrication threshold less relevant as quantitative measure since each of the architecture requires optimisation of the exposure parameters. Here is another direction of parametric studies where Deep Learning (Artificial Intelligence) can be of great use⁶⁵. Current findings provides an important database of experimentally validated 3D photopolymerization at nano-scale results offered with qualitative description of energy deposition, which is enhanced at nanoscale. It is expected that no-PI structuring can help mitigate the proximity effects in high-resolution feature-dense objects or explore the projection lithography arrangements⁶⁶. Indeed, no proximity effects are present in nano-field ablation⁵⁹ based on the light localisation discussed here for the polymerization case.

As take away message could be that depending on the absorption and sensitivity of the material and by adjusting the laser exposure fabrication parameters one can achieve wavelength independent structuring. Thus, this way empowering not only material-to-laser optimization, but the opposite – laser intensity adjustment to match the conditions required for localized controlled photo-cross-linking. Excluding PIs increases the used optical fabrication power (exposure dose), but the use of organic materials (like pure acrylic resins) could enable realization of lower fabrication powers than SZ2080^TM, thus extending the MPL established photoresist library²².

Here we draw a few conclusions as experimentally validated important points for a take away:

1. Photo-structuring of non-sensitized pre-polymer materials is possible via X-photon route using various VIS and NIR wavelengths of common femtosecond laser oscillators operating at sub-1 nJ/pulse and tens-of-MHz repetition rate).

2. The pulse amplification or specific wavelength is not critically essential, thus allows usage of high-rep rate laser sources providing nJ and even pJ energies per femtosecond pulse.

3. 780 nm wavelength allowed fabrication in different hybrid organic-inorganic concentration host materials offering comparable features with the photo-sensitized resins.

4. 517 nm wavelength empowered rapid fabrication reaching 10⁵ µm/s translation velocities which is current state-of-the-art for the commercial workstations and photopolymers.

5. 1035 nm wavelength enabled photopolymerization yet limited structuring capacity, which required precise adjustment of parameters to slow scanning speeds (still comparable to STED-inspired or photoreduction processes). On the other hand using dry objective lenses the additive manufacturing could also be realized.

6. The absence of PI in a photoresist suitable for MPL proved to be not a serious limitation for its processing but rather a straightforward improvement in performance. Without addition of PI the DFW decreased by a factor 2 - 4 depending on the inorganic-organic composition ratio. With further studies it is expected to be beneficial in reducing the proximity effect in high-resolution densely filled architectures.

7. Finally, considering the low auto-fluorescence of the non-photosensitized SZ2080^TM, it provides evidence that the absence of PI can yield promising results in various applications where fluorescence is a limiting factor - microscopy, biology, micro-optics, and nano-photonics.

In summary, the findings reveal that versatility of fs-pulses to deliver the energy into confined volume and cause photo-crosslinking reactions almost independently on applied wavelength and used material. This extends the advantages of two-photon polymerization beyond two-photon absorption as a distinct light-matter interaction condition. The achievements are offering novel approaches to exploit new laser sources and beam parallelization / exposure projection means for improving additive manufacturing throughput without sacrificing resolution or trade-offs in materials functionality^{67, 68}. Control of energy deposition into nano-sized volumes via optical near-field enhancement, comparable with the enhancement in nanogaps between plasmonic nanoparticles, is realised by photo-ionisation and generation of free electrons plasma at the very tip of the intensity envelope at the center of focal spot. Such dip in refractive index becomes location of energy deposition and is writing nano-pen for 3D printing. Control of local permittivity of host polymer defines the energy deposition and 3D polymerization. This is the reason why actual focal volume (linear intensity distribution) becomes less relevant as a 3D exposure block for filling the required volume. 3D energy deposition is sub-diffraction limited by its essence at high light intensity of $ \sim 1 $ TW/cm$ ^2 $.

Materials Synthesis. The material used was SZ2080^TM without PI and compared results obtained with the well-known PI Michler’s ketone (4,4'-bis(diethylamino)benzophenone). The material was synthesized using Methacryloxypropyl trimethoxysilane (MAPTMS, 97%), zirconium n-propoxide (ZPO, 70% in propanol) and Methacrylic acid (MAA, 99%). All materials were purchased from Sigma-Aldrich (Steinheim, Germany) and were used without any purification. A variety of ZPO: MAA molar concentrations were synthesized varying from 1:1 to 1:4, while the molar ratio for MAPTMS: ZPO was 8:2. The molar concentration of the non-photosensitized SZ2080^TM that was used for the fabrication of all the 3D structures was 1:1.

Sample preparation. For sample preparation for the laser structuring, the synthesized material was drop-cast on thin glass substrates (thickness: 120 µm and diameter: 13 mm) and the droplets were placed in vacuum at room temperature for 3-4 days or followed a heating procedure in 90$ ^\circ $C for up to 40 min for densification by solvent removal. The densification step leads to the evaporation of the solvents which results in the minimization of the shrinkage during laser exposure and the final development. After fabrication of 3D structures, the droplets were developed using 4-methyl-2 pentanone for 30 min in ambient laboratory conditions.

Experimental setup for 780 nm fs-laser oscillator. The fabrication of 3D-microstructures using a femtosecond fiber laser (FemtoFiber pro NIR, Toptica Photonics AG) emitting at 780 nm (pulse duration 150 fs, average output power 500 mW and repetition rate 80 MHz) was made with two different setups (see, Supplement Fig. S1, S2, in order to study the resolution and the fabrication repeatability of the non-photosensitized SZ2080^TM69.

Specifically, the Nano setup was used to investigate the resolution of the material via fabrication of 3D woodpiles. For ease of reference, we refer to it as Nano as it employs piezo-electric stages capable to move in the XYZ axes (Physik Instrumente, M-110.1DG, Germany), up to 100 $ \mu $m, while the laser beam is stable and is focused by a microscope objective lens 100x/1.4 NA (Plan Apochromat, oil-immersion lens (Zeiss, Germany).

The Galvo setup was used to investigate the power thresholds in combination of different material concentrations and dimensions. We refer to it as Galvo to due to the fact that a galvanometric mirror system (Scan- labs Hurryscan II) is used in order to scan the laser beam inside the material on the XY-plane, while a linear translation stage moves the sample in the Z-direction (Physik Instrumente M-500, Germany). The microscope objective lenss that focused the beam into the material, was a 40×/0.95 NA (Plan Apochromat, Zeiss, Germany).

Experimental setup for 517 nm and 1035 nm fs-laser oscillator Simplified setup in which either fundamental 1035 nm Yb-based oscillator exposure or second harmonic (517 nm) wavelengths can be employed for MPL is presented in more details in Fig. S3, where fs-laser is delivering ~ 100 fs duration pulses at a 76 MHz repetition rate. Focusing in this system was achieved by 63x/1.4 NA oil objective lens (Plan- Apochromat, Zeiss) using Immersol^TM 518F immersion oil.

Photoluminescence measurements The photoluminescence measurements were carried out using a He–Cd CW-laser at 325 nm with full power of 35 mW. The beam was focused onto the samples by a fused silica lens with focal length 4 mm. The spot size of the focused laser beam was 80−100 µm. The samples for the photoluminescence measurements were 3D cubes (dimensions: 125 × 125 × 15 µm³), on a quartz substrate, fabricated with the non-photosensitized SZ2080^TM, with the molar ratio of ZPO:MAA= 1:1.

Scanning electron microscopy Morphological analysis of the samples developed using the 780 nm laser oscillator was performed by SEM (JEOL JSM-6390LV, JEOL Ltd., Akishima, Tokyo, Japan) operating at 20 keV. The 3D structures were sputtered with 10 nm Au coating. For structures fabricated using 517 nm and 1035 nm exposures, Hitachi TM-1000 SEM operating at 15 keV was used, while samples were coated with 20 nm Ag.

This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 101007417, having benefited from the access provided by FORTH in Two-photon Lithography (TWL), Scanning Electron Microscopy (SEM), PhotoLuminescence (PL) within the framework of the NFFA-Europe Pilot Transnational Access Activity, proposal [ID-077]. The research leading to these results has received funding from LASERLAB-EUROPE (grant agreement no. 871124, European Union’s Horizon 2020 research and innovation programme). A.B., E.S. and M.M acknowledge Vilnius University Excellence Initiative programme, and S.J. under Adjunct agreement as Visiting Professor for mutual research activities with the Laser Research Center of the Faculty of Physics of Vilnius University. Furthermore, part of this work was co-financed by Greece and the European Union (European Social Fund-ESF) through the Operational Programme “Human Resources Development, Education and Lifelong Learning” in the context of the Act “Enhancing Human Resources Research Potential by undertaking a Doctoral Research” Sub-action 2: IKY Scholarship Programme for Ph.D. candidates in the Greek Universities. The research project was co-funded by the Stavros Niarchos Foundation (SNF) and the Hellenic Foundation for Research and Innovation (H.F.R.I.) under the 5th Call of “Science and Society” Action – “Always Strive for Excellence – Theodore Papazoglou” (Project Number: 9578.) Dr. Darius Gailevičius (VU LRC) for indispensable help in laboratory and discussing the experimental flow. Maria Androulidaki (FORTH) for conducting the Photoluminescence measurements. Aleka Manousaki (FORTH) for the SEM images.