-
Magnetorheological finishing (MRF) has been widely used in the ultra-precision fabrication of plane, spherical, aspherical, and some free-form optical elements1-4. A variety of materials can be polished up to the nanometer level with MRF. The surface accuracy and quality after MRF can satisfy the requirements of optical systems used in industrial, high-power lasers, medical or semiconductor optics5,6. It is known that MRF technology involves the interdisciplinary of electromagnetics, chemistry, rheology, and contact mechanics. The shear force generation mechanism during the polishing process and have not been elucidated and the present material removal model is not instructive enough for the study of MRF.
Extensive research has been conducted to reveal the material removal mechanism of MRF. A.B. Shorey adopted Bingham fluid model and proposed that material removal depends on the shear stress over the workpiece based on the fluid lubrication theory7. This is a preliminary study on the MRF material removal mechanism. Kordonski built a material removal model based on the Preston equation by introducing a modified Preston coefficient8. The established model shows the relationship between the material removal rate and normal force, which depends on the friction coefficient and normal pressure on the workpiece during the polishing process. They proposed that the normal force and shear stress over the workpiece during the polishing process arise from the hydrodynamic pressure between the polishing fluid and the workpiece.
However, A. B. Shorey discovered that the hydrodynamic pressure of the polishing powder during processing is too low to achieve efficient material removal and proposed that the material removal efficiency is proportional to the shear stress on the workpiece, in subsequent research9. Lambropoulos reported that material removal efficiency is linearly related to the mechanical properties (grinding figure of merit) of the polished materials10. DeGroote built a material removal rate model for glasses by carrying out large numbers of experiments11. The model covers the effects on the material removal rate of the concentration and size of the iron powders and abrasives used in the MR polishing fluid, the processing force on the workpiece surface, the pH of the fluid, the mechanical parameters of the polished material, and the surface energy. However, there is still a large deviation between the model and the experimental results considering only the peak removal rate. Therefore, the established model cannot be applied to predict the MRF material removal rate. Miao used the spot taking machine (STM) to study the process force on a workpiece during the MRF process12,13. The normal pressure and shear force on the workpiece in polishing BK7 glass and alumina nitride ceramics (ALON) were measured under different process conditions. It was also found that the material removal rate was approximately linear with the shear stress on the workpiece, the friction coefficient in polishing ceramics was basically constant, and the friction coefficient in polishing glass was variable, but the reason was not clear. The generation mechanism of the shear force during polishing was not presented. Kordonsiki proposed that the force generating the material removal of MRF is due not to the hydrodynamic pressure from the MR polishing fluid, but to the severe collision of iron powder particles and abrasives in the polishing area, which resulted in a large shear force over the contact area of the workpiece surface14. Markus Schinhaerl established a mathematical model for the MRF removal function based on the contact model and removal function experiments. The model can predict the removal function distribution under specific process parameters15,16. Liu calculated the hydrodynamic pressure and built the removal function model based on Preston function17. Then, an interactive regionalized modeling approach of tool influence function for the processing of aspherical optics was proposed.
Previous research has demonstrated that the material removal of MRF depended on the shear stress over the workpiece in the polishing area, and the shear stress can be influenced by the composition of the MR polishing fluid and process parameters, such as the magnetic field strength, penetration depth, et al. However, the mechanical properties of the MR polishing fluid change under a high shear rate in the polishing process18−20. These changes arise from the microstructure breakdown of the MR polishing fluid in the converging gap, which develops into the sheared particle flow that consists of particles added to the MR polishing fluid. Meanwhile, the normal force from the unsheared core attached to the wheel will influence the sheared flow, which means that the surface abrasion (material removal rate) will be different as the normal force changes. This should be fully considered, especially in the processing of complex surfaces with MRF. Therefore, a new principle should be introduced to reveal the material removal mechanism of MRF and further optimize the process parameters and MR polishing fluid.
Based on the measurement and analysis of the rheological characteristics of the MR fluid under a high shear rate, we proposed to divide the MR polishing fluid in the polishing area into a shear thinned dense granular flow and a magnetized core that is attached to the polishing wheel without shearing. According to the removal function experiments and processing force test, a novel theoretical model of the MRF removal function was established based on the dense granular flow theory. The established model can simply realize the decoupling of the MRF processing parameters effectively. The results of this study have important theoretical significance in the research and application of MRF technology.
-
The MR polishing fluid is mainly composed of a low-viscosity base carrier (usually water), iron particles, and abrasives. The size of the iron powders used in the MR polishing fluid is 1–10 μm and the size of the abrasives is much smaller. Nanometer-sized diamond or cerium oxide is usually used depending on the processing material. In the polishing process, the MR polishing fluid is magnetized as rotating with the polishing wheel to the polishing area. The uniformly dispersed iron powders and abrasives are rearranged, showing the characteristics of a viscoplastic body under the action of a magnetic field. The shear and compression contact between the MR polishing fluid and workpiece in the polishing process results in fluid structural remodeling, and the magnetization chain of iron particles become closer and strengthened. The abrasives are separated from the magnetized MR fluid ribbon interior to the surface under the gradient magnetic field and by scratching the workpiece surface in the polishing area, which resulted in material removal. During the polishing process, the MR polishing fluid is subjected to a high shear rate (> 500/s). Therefore, the rheological behavior of the MR polishing fluid under a high shear rate plays a key role in the material removal mechanism of MRF.
A commercial magneto-rheometer (MCR302) was used to analyze the rheological properties of the MR polishing fluid during the polishing process. The storage modulus and shear modulus under shear in the oscillation mode were investigated by adopting the commonly used MR polishing fluid. The median size of the iron particles (carbonyl iron powders) used was 4 μm and the volume content was 40%. The abrasives used in the fluid were nano-diamond, with a median size of 100 nm and a volume content of 0.1%. The base carrier liquid was deionized (DI) water. Scanning electron microscopy (SEM) images of the iron particles and nano-diamond used in the MR polishing fluid are shown in Fig. 1.

Fig. 1 Scanning electron microscopy (SEM) images of iron powders a and abrasives b used in the magnetorheological (MR) polishing fluid.
The rheological measurement conditions adopted were a magnetic field strength of 250 kA/m, an oscillation frequency of 2 Hz, a rotor diameter of 20 mm, and a distance of 1 mm between the rotor and test disk. The testing results of the storage modulus and shear modulus under dynamic oscillation mode are shown in Fig. 2. The results show that when the MR polishing fluid is subjected to a low shear rate, its storage modulus and shear modulus are approximately 0.82 and 0.95 MPa, respectively, which means that the MR fluid shows elastic properties at this state. However, when the shear strain increases, the storage modulus and shear modulus decrease sharply, which means that the shear force between the rotor and the magnetized MR fluid is greater than its shear yield stress, and the MR fluid is sheared and thinned to form a sheared granular flow with a further increase in shear rate14.
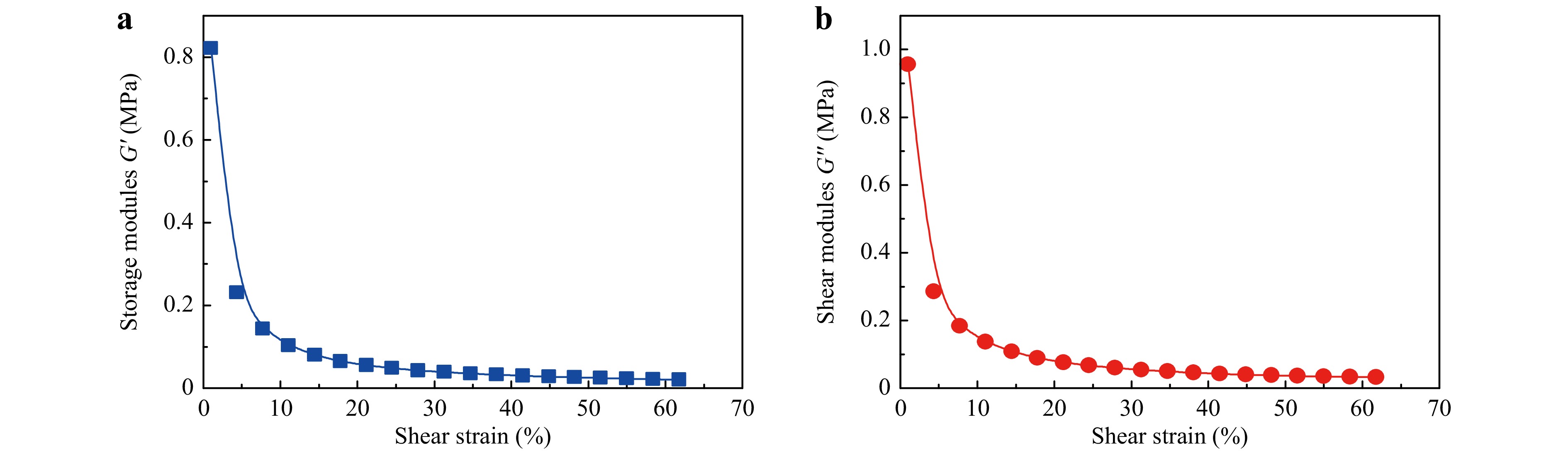
Fig. 2 Rheological properties of the MR polishing fluid under oscillation mode: a shear strain - storage modulus diagram; b shear strain - shear modulus diagram.
However, in an actual polishing process, the MR polishing fluid in contact with the workpiece is not completely shear thinned. The rim of the magnetized MR polishing fluid in contact with the workpiece is shear thinned, but the bulk of the MR polishing fluid attached to the polishing wheel undergoes structural reconstruction under extrusion. Thus, the magnetization chains become shorter and with denser stacking, resulting in a viscoplastic body. Therefore, the rheological properties of the sheared granular flow formed by the MR polishing fluid and the properties of the unsheared magnetized solid-like body will determine the material removal rate and the removal function distribution of MRF. Therefore, it is crucial to elucidate the generation mechanism of the shear force on the workpiece, in the MRF process, and establish a theoretical model of the removal function.
-
The MR polishing fluid circulates along with the rotation of polishing wheel in the actual polishing process, and the abrasives seep from the MR polishing fluid under the magnetic field effects in the polishing area. Owing to the small distance between the polishing wheel and the workpiece, the magnetized MR polishing fluid is squeezed and sheared. This effect causes the rearrangement of the magnetized structure, resulting in a wide and thin fluid ribbon. As a result, there exists a large shear force between the MR polishing fluid and the workpiece owing to the rotation of the polishing wheel, which results in the removal of material from the workpiece. Based on the rheological characteristics of the MR polishing fluid under a high shear rate and the coupling relationship of multiple parameters under the actual polishing state, we considered the sheared thinned particle flow that contacting the workpiece as a dense granular flow, whereas the unsheared magnetized solid core after extrusion and reorganization is regarded as a viscoplastic body in this study.
-
Dense granular flows are widely used in tribology, powder metallurgy, hydropower engineering, geological hazards, and other fields21,22. A dense granular flow is a particle system composed of large numbers of discrete solid particles that are generally static when there is no external disturbance. However, when the system is subjected to external shear, vibration, rotation, or fluid disturbance, the system exhibits a flow phenomenon similar to that of a liquid. The dense granular system shows the rheological properties of a plastic body as a whole23,24. In contrast to the classical Bingham fluid or Herschel–Bulkley fluid, the special feature of a dense granular flow is that the effective viscosity depends on both the shear rate and the confining pressure. This feature is embodied in the frictional property of a granular flow medium under pressure25,26. Therefore, we constructed a schematic diagram of the interaction between the MR polishing fluid and the workpiece in the MRF polishing process, as shown in Fig. 3.
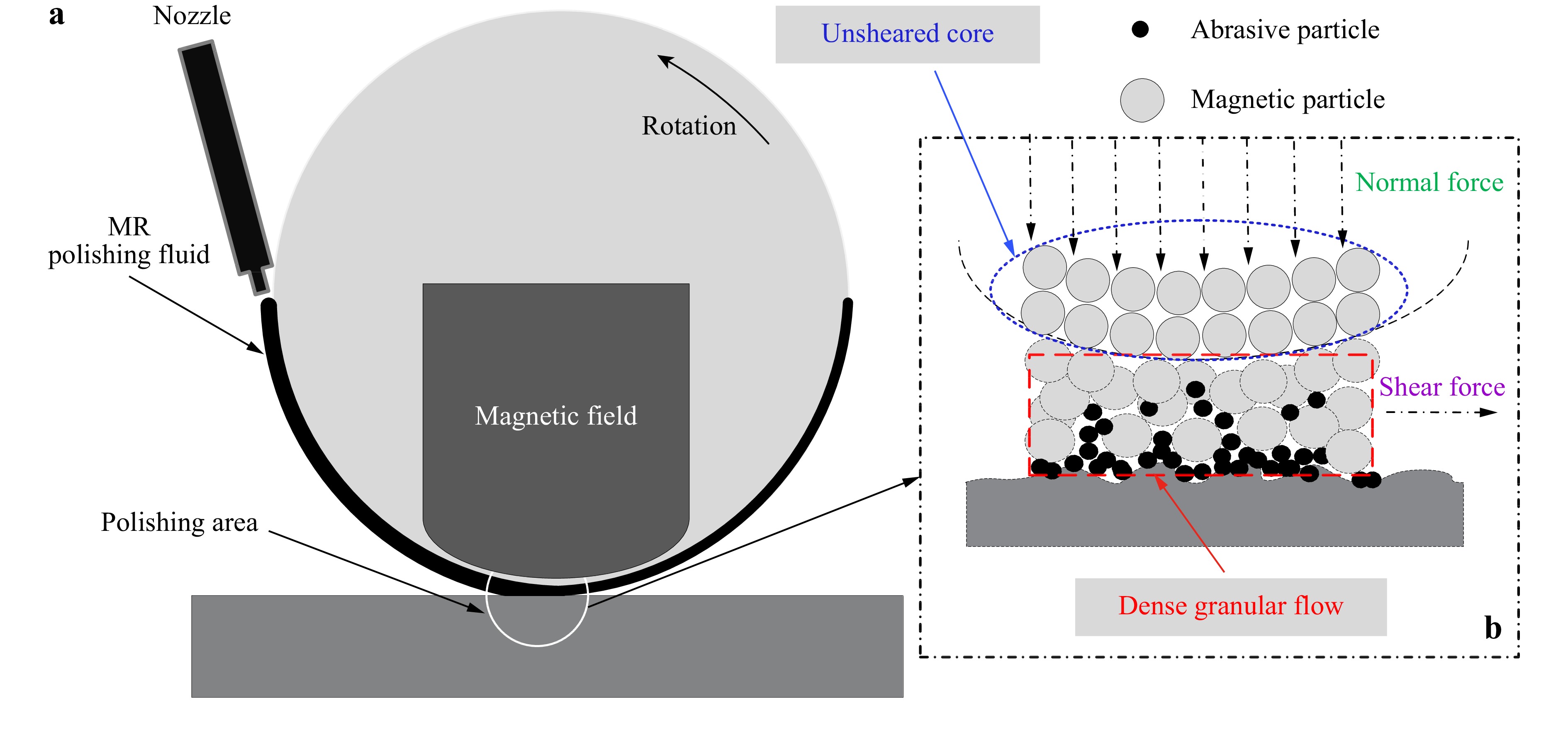
Fig. 3 The shear force generation mechanism of MRF:a contact model of MRF; b the rheological behavior and interaction of MR polishing fluid with workpiece in polishing area.
Based on the rheological properties of the MR polishing fluid, we divided the polishing fluid in the polishing area into two layers, as shown in Fig. 3b. The interior layer attached to the wheel, which is a magnetized solid-like core, and the outer layer of the MR polishing fluid in contact with the workpiece, which changes to a dense granular flow under the high shear rate. Under the actual polishing state, tangential sliding exists between these two layers. The magnetized solid-like core is squeezed, and the generated normal force acts upon the shear dense granular flow (which consists of iron particles, abrasives, and carrier fluid) in the polishing area. Therefore, this normal force directly influences the interaction characteristics between the granular flow and workpiece. The results are reflected in the friction characteristics at the contact interface and the shear force over the workpiece, during the polishing process27.
-
It is known that the material removal of the MRF depends on the shear force over the workpiece surface. According to the rheological analysis and actual polishing contact model, the shear stress over the workpiece is determined by the normal pressure from the unsheared magnetized core and friction over the workpiece arising from the sheared dense granular flow. The solid particles (abrasives and carbonyl iron powders) used in the MR polishing fluid are not standard frictionless spherical particles. Therefore, the shear stress can be written as shown in Eq. 1 according to the constitutive law of dense particle flow.
$$ \begin{split}&\tau = \mu ({I_m})P\\& \mu ({I_m}) = {\mu _0} + \beta {I_m^\alpha} ,\;{I_m} = \mathop \gamma \limits^ \cdot \overline d(p/\overline \rho_s)^{-0.5}\end{split} $$ (1) where τ is the shear stress, μ(Im) is the friction coefficient, Im is the modified inertial number of dense granular flow, α is the parameter related to the particle shape and surface properties, β is a parameter that depends on the MR fluid rheological properties, P is the pressure acting upon the dense granular flow, d and ρs are the average particle size and density of the particles, respectively, and
$ \dot{\gamma } $ is the shear rate of the granular flow. During the polishing process, the granular flow is in an equilibrium state, and the sheared thinning granular flow velocity is close to the magnetized core velocity, which is consistent with the speed of the polishing wheel. However, it is different from Preston equation, the influence of granular flow velocity on removal function is reflected through shear rate based on granular flow theory.Therefore, corresponding to the MRF process, τ is the shear force over the workpiece surface during the polishing process, and μ(Im) is the effective friction coefficient of the interface between the MR polishing fluid and the workpiece over the polishing area. P is the normal pressure on the granular flow formed by the sheared thinning MR polishing fluid. P depends on the mechanical and rheological properties of the MR polishing fluid under squeezing and shear after magnetization. Therefore, it is necessary to acquire the normal pressure distribution and effective friction coefficient over the workpiece to build a shear stress model and material removal model of the MRF.
-
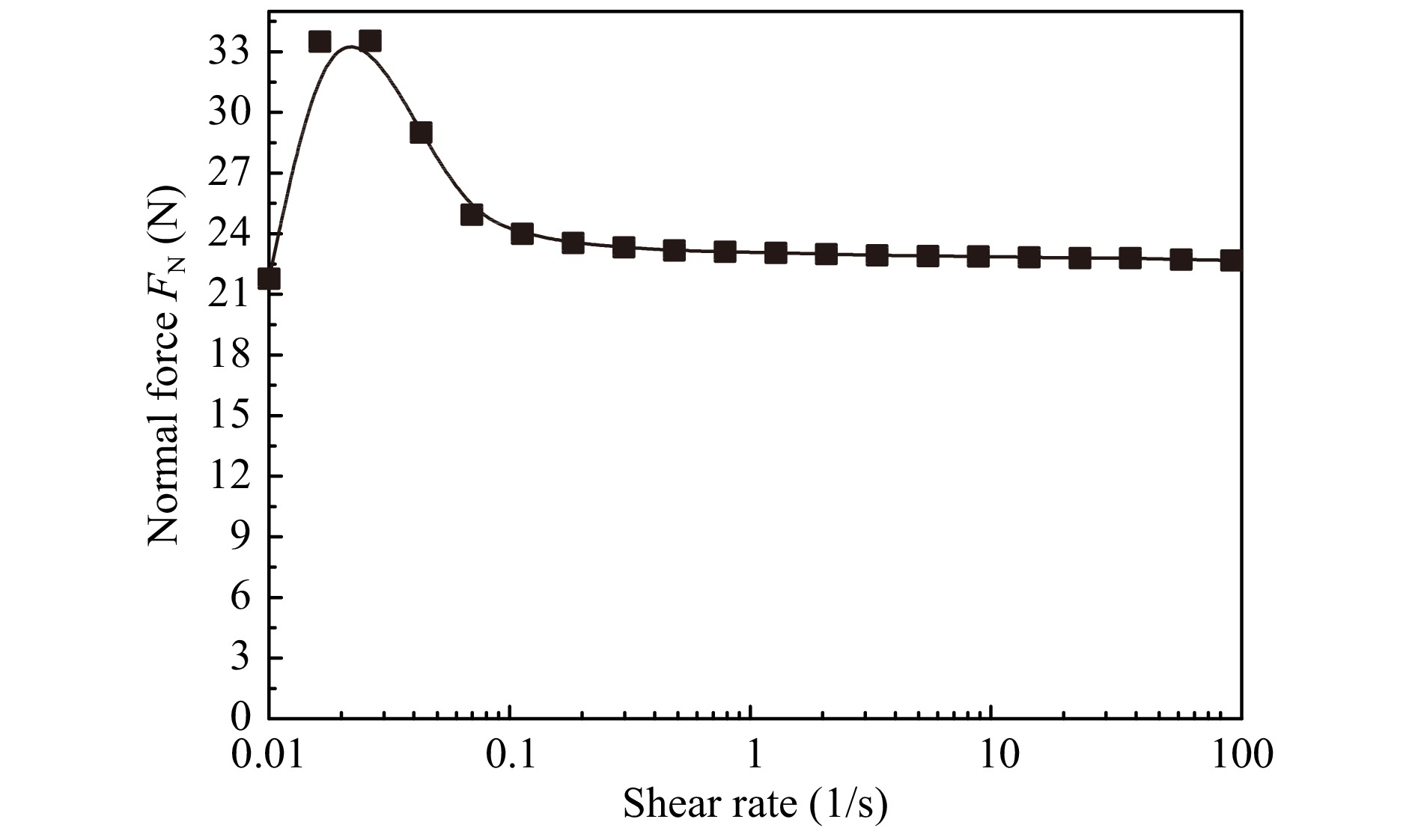
As a result, the MR fluid exhibits rheological properties similar to those of a viscoplastic body under a high shear rate in the polishing state. The solid-like magnetized core of the MR polishing fluid attached to the polishing wheel will be in the squeeze state in an unlimited space. Considering that the magnetic field in the polishing area is not a uniform magnetic field, we analyzed the normal force under the magnetic field with a magnetorheometer (MCR-302) because the magnetic field intensity distribution of the MR testing module is close to the magnetic field generation module of the MRF. Therefore, it can accurately reflect the normal force characteristics of the MR polishing in the actual polishing process. According to the typical process parameters presented in Table 1, the normal force characteristics of the MR fluid under different shear rates were tested using a magnetorheometer, and the results are shown in Fig. 4.
Parameters Wheel diameter/mm Rotate speed/
(r/min)Rate of flow/
(ml/min)Value 160 120 480 Table 1. Typical process parameters
The normal force of the MR fluid gradually increases under a low shear rate. However, when the shear rate exceeds 0.3/s, the MR fluid contacting the moving wall exhibits solid–liquid conversion and solid particle rearrangement, which results in a gradual decrease in the normal pressure. As the shear rate increases further, the normal force gradually decreases and tends to the initial normal force, which is quasistatic. Thus, the normal force from the unsheared solid-like core in the MRF process can be expressed based on the continuous media theory 28,29.
Therefore, the force acting on the sheared thinning MR polishing fluid can be expressed as shown in Eq. 2 according to the polishing parameters and fluid rheological properties.
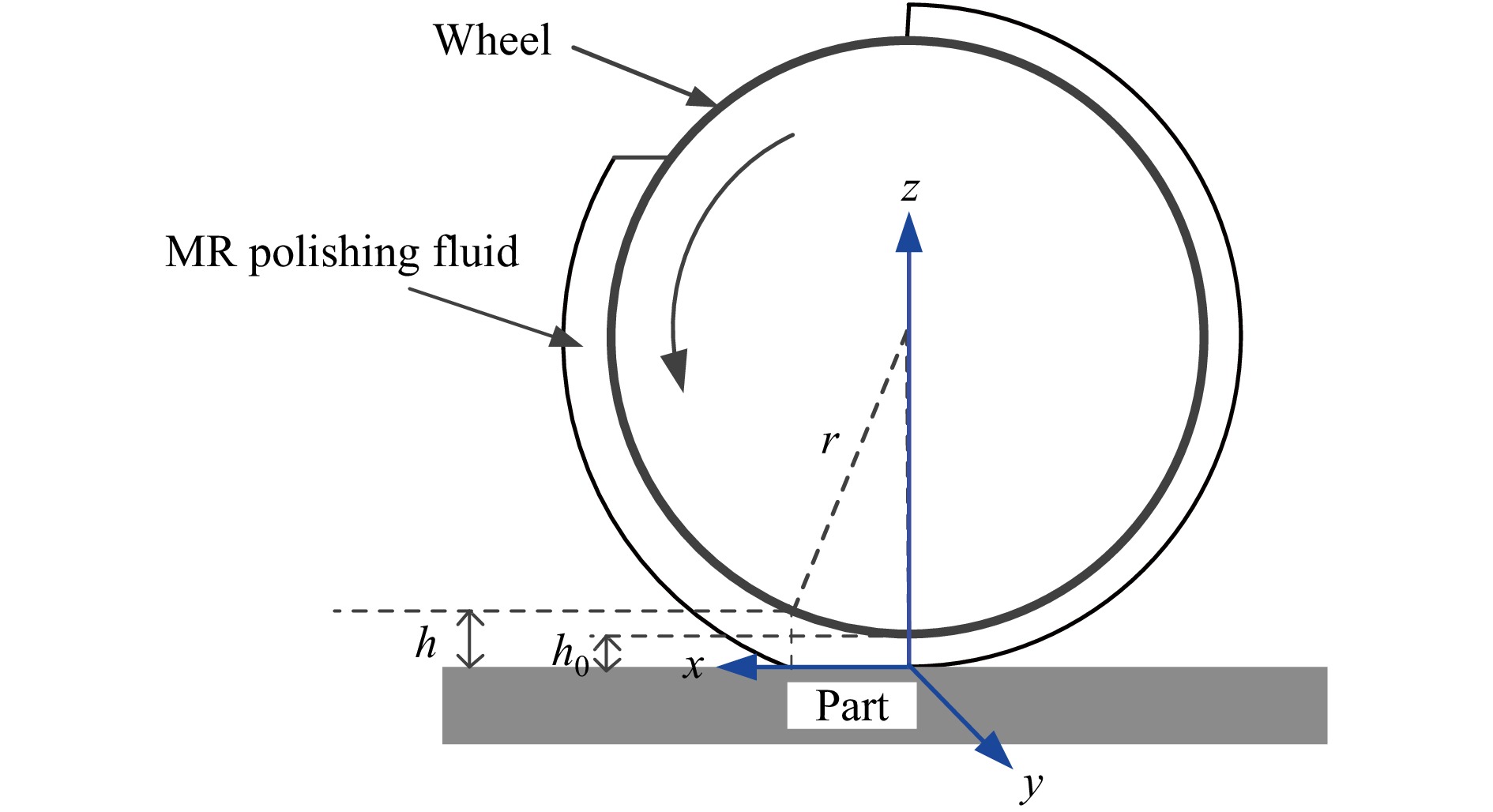
$$ {F_N} = \frac{a}{{{h^{n - 1}}}} - \frac{b}{{{h^n}}} + \delta $$ (2) where a and b are coefficients that depend on the volume and shear yield stress of the MR polishing fluid, h is the gap distance, and δ is the modification parameter of FN under a non-uniform magnetic field. The parameter n is determined by the rheological properties of the MR polishing fluid, magnetic field strength, and polishing parameters. Based on the MRF process contact model shown in Fig. 5, h1 is the initial thickness of the MR fluid ribbon before contact with the workpiece, and h0 is the thickness after exiting from the polishing area. R is the radius of the polishing wheel.
Therefore, the normal force FN along the x-coordinate can be approximately expressed by the following equation:
$$ {F_N}{\text{ = }}\frac{a}{{{{\left({h_0} + \dfrac{{{x^2}}}{{2R}}\right)}^{n - 1}}}} - \frac{b}{{{{\left({h_0} + \dfrac{{{x^2}}}{{2R}}\right)}^n}}} + \delta $$ (3) -
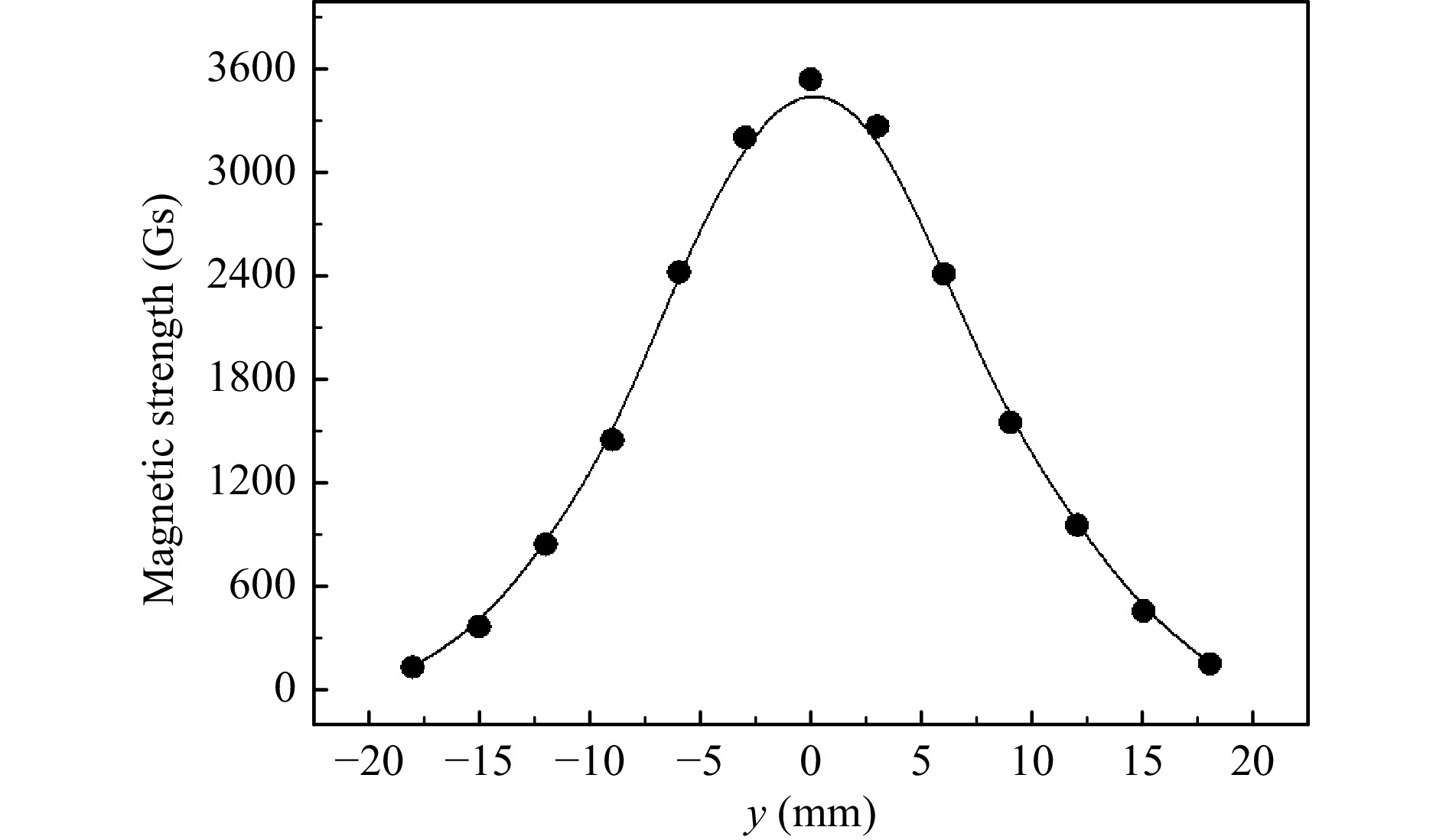
According to the dense granular theory, the effective friction over the contact area depends on the normal pressure, particle size distribution, density, and shear rate. The magnetic confinement pressure of MRF is different from that of a regular sheared granular flow. Removal function experiments were carried out with self-developed MRF polishing machine based on permanent magnetic generator. The gradient magnetic strength and distribution over the polishing wheel surface along the y direction according to the contact model (Fig. 5) is shown in Fig. 6
The process force is measured with the Kistler force sensor, and the spot area and removal rate were calculated based on the testing results with interferometry. The process parameters are presented in Table 1.
According to the previous experimental results, the initial MR fluid ribbon height, corresponding to h1 shown in Fig. 5, was 2.0 mm with the typical processing parameters. The normal force, shear force, and removal function area under different working gaps h0 were measured through a removal function experiment with BK7 glass. The results are presented in Table 2.
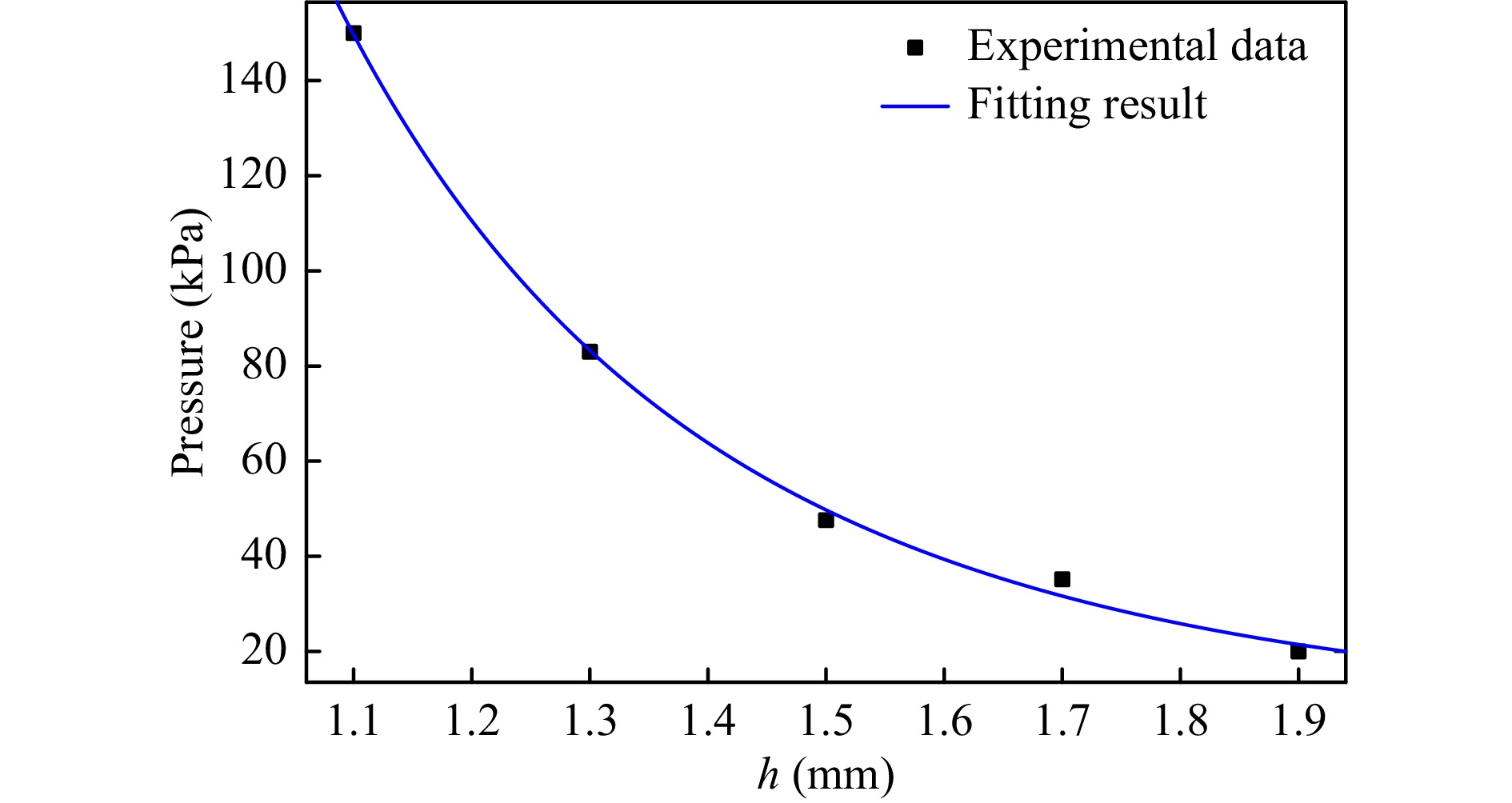
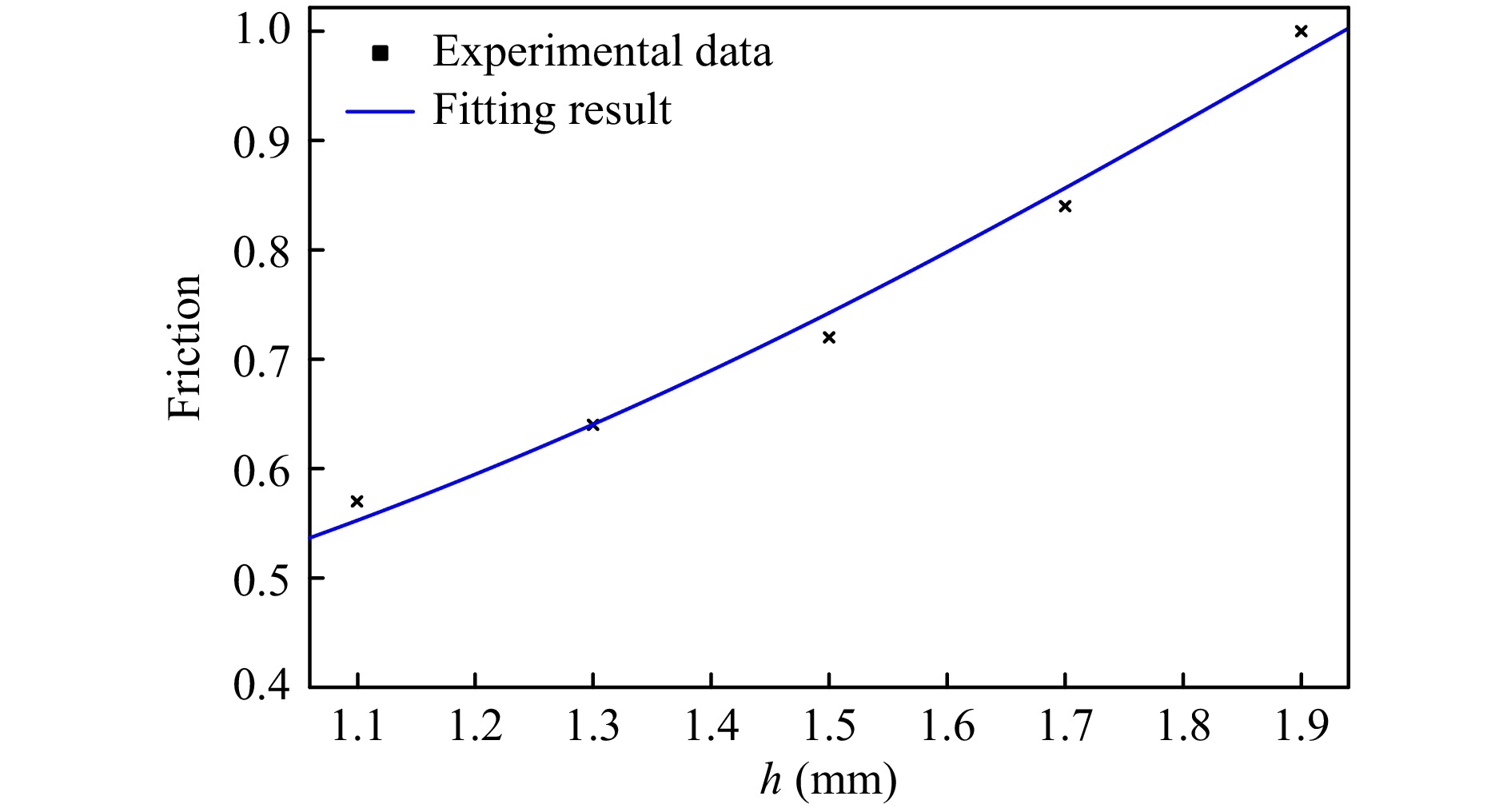
working gap/mm Shear force/N Normal force/N Effective Friction (μ) Spot area/mm2 Normal pressure/kPa 1.1 3.2 ± 0.05 6.7 ± 0.05 0.48 44.5 ± 0.5 150 1.3 1.92 ± 0.05 3 ± 0.05 0.64 36.5 ± 0.5 83 1.5 0.94 ± 0.05 1.3 ± 0.05 0.72 27.3 ± 0.5 47.6 1.7 0.54 ± 0.02 0.64 ± 0.02 0.84 18 ± 0.5 35.16 1.9 0.12 ± 0.01 0.12 ± 0.01 1 6 ± 0.2 20 Table 2. Effect of working gap on processing force and spot area
The normal force depends on the working gap and has a decisive influence on the inertial number of a granular flow consisting of a sheared thinned MR polishing fluid in the polishing area. According to the results listed in Table 2, Fig. 7 shows the normal pressure under different working gaps and the fitting results with Eq. 2. This result also demonstrates the pressure along the long axis of the removal function owing to the changes in penetration depth.
According to the fitting results, we can obtain the coefficients a = 292, b =85, and n = 5, δ ≈ 0. The R-square (coefficient of determination) is 0.9992 and the RMSE (root mean squared error) is 17.75 with the fitting equation. Considering the MR polishing fluid composition and properties, the coefficient α can approximate to 1 for a sheared granular flow in the polishing area based on the granular flow theory and the effect of shape and friction of particles of the granular flow. Therefore, the modified inertial number Im in Eq. 1 can be simplified as follows:
$$ \mu = {\mu _0} + A{P^{ - 0.5}},\begin{array}{*{20}{c}} {} \end{array}A{\text{ = }}\beta \frac{{\mathop \gamma \limits^ \cdot \overline d }}{{\sqrt {k\overline {{\rho _s}} } }} $$ (4) Based on Eq. 4 above and the friction results listed in Table 2, we can obtain the fitting results of friction under different working gaps, as shown in Fig. 8. The fitting results show that μ0 = 0.38 and A = 2. The R-square (coefficient of determination) is 0.991 and the RMSE (root mean squared error) is 0.0165 with the fitting Eq. 4. These results demonstrate the effective friction under different working gaps during MRF process.
-
As shown in Fig. 3, there is a division of the filler particles under the magnetic impact in the polishing area: magnetic particles are attracted to the polishing wheel, and abrasive particles are gathered in the surface layer. The removal of material is due to the cutting of the surface roughness by the sharp edges of abrasives moving with the MR polishing fluid. Therefore, the abrasive concentration over the polishing area affects the material removal rate and removal function profile. The concentration distribution of dispersed particles of the MR polishing fluid in the gap between the workpiece and polishing wheel can be simulated based on the Boltzmann law30. The abrasive particle number Nc in the sheared layer along x under typical process parameters can be expressed as follows:
$$ {N_c}(x) = {N_a}\frac{{1 - exp\left[ - {m_a}{g_a}h{{\left(\dfrac{{2\eta {t_r}}}{{3n}}{{\mathop \gamma \limits^ \bullet }^2}\right)}^{ - 1}}\right]}}{{1 - exp\left[ - {m_a}{g_a}((R + {h_1}) - h){{\left(\dfrac{{2\eta {t_r}}}{{3n}}{{\mathop \gamma \limits^ \bullet }^2}\right)}^{ - 1}}\right]}} $$ (5) where Na is the abrasive concentration of the MR polishing fluid, ma is the mass of the abrasive particle, and ga is the acceleration of the motion of the abrasive particles under the influence of the magnetic volume force. R is the radius of the polishing wheel, η is the viscosity of the base MR base fluid,
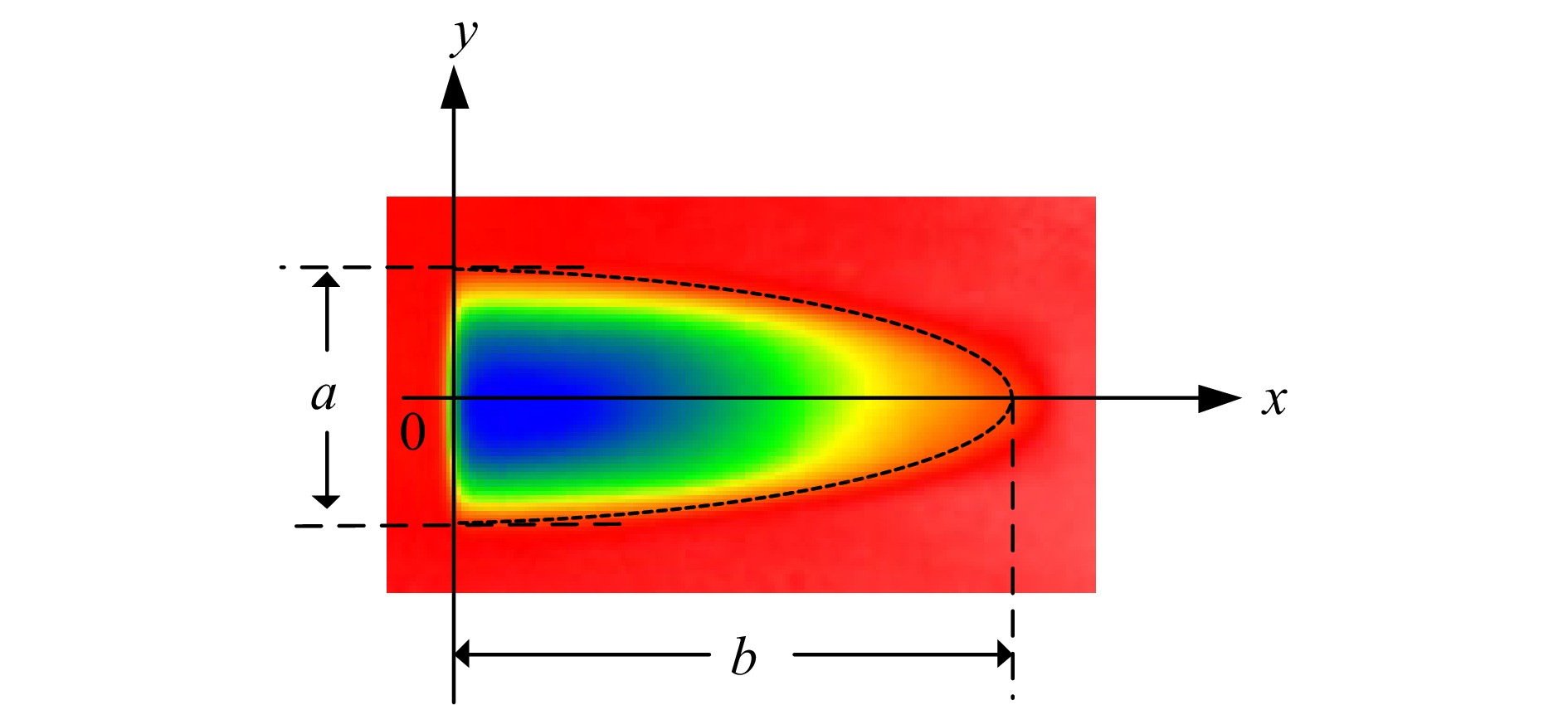
$ \dot{\gamma } $ is the shear rate, tr is the relaxation time, and n is the number of abrasive particles in the contact bulk over the polishing spot.The number of abrasive particles that contact the workpiece is also influenced by the removal function spot shape. The shape parameter of a typical MRF removal function is shown in Fig. 9. The length and width of the removal function are a and b, respectively, and the outer contour of the removal function is approximately parabolic.
Therefore, the outer contour of removal function can be expressed as follows:
$$ y = \sqrt {\frac{{{a^2}}}{{4b}}(b - x)} $$ (6) Based on Eq.5, 6, we can obtain the abrasive
particle concentration Ca along the long axis of the removal function:
$$\begin{split} {C_a} =& {N_a}\frac{{1 - exp\left[ - {m_a}{g_a}\left({h_0} + \dfrac{{{x^2}}}{{2R}}\right){{\left(\dfrac{{2\eta {t_r}}}{{3n}}{{\mathop \gamma \limits^ \bullet }^2}\right)}^{ - 1}}\right]}}{{1 - exp\left[ - {m_a}{g_a}\left((R + {h_1}) - \left({h_0} + \dfrac{{{x^2}}}{{2R}}\right)\right){{\left(\dfrac{{2\eta {t_r}}}{{3n}}{{\mathop \gamma \limits^ \bullet }^2}\right)}^{ - 1}}\right]}}\\&{\left(\frac{{{a^2}}}{{4b}}(b - x)\right)^{ - \frac{1}{2}}} \end{split}$$ (7) -
It is known that the MRF material removal rate depends on the shear stress over the polishing area. In contrast to the traditional Preston equation, the normal pressure is substituted by shear stress over the polishing area, and the polishing velocity is considered as an impact factor on the inertial number in this study. The shear stress calculated based on the granular flow decouples the complex influence parameters on the MRF material rate from a new perspective. Thus, the MRF material removal model can be expressed as follows:
$$ MRR = C\tau = {C_{MRF}}\mu {F_N} $$ (8) CMRF is the coefficient of the theoretical material removal rate based on the granular theory. The parameter CMRF is mainly determined by the mechanical merits of the workpiece, abrasive concentration, particle size distribution, and properties. In this study, we focus on the profile of the removal function from the inlet to the lowest point of the MR fluid ribbon under the wheel (from 0 to b), which can reveal the material removal mechanism and the main factors influencing the MRF process. Therefore, we can obtain the novel material removal model based on Eq. 3, 4, 7, 8, and the material rate of MRF along x (long axis) can be expressed as Eq. 9.
Under the typical polishing parameters, h0 = 1 mm, the polishing wheel radius R = 80 mm, and the removal function size coefficients a ≈ 6 mm and b ≈ 13 mm. The iron particle used in the MR polishing fluid is carbonyl iron with a density ρm = 7.5 × 103 kg/m3, average magnetization Jm = 5 × 105 A/m, and median size of d = 2 × 10−6 m. The abrasive particles used in the MR polishing fluid are nano-diamond with a volume concentration of 0.1 vol%, the particles of which have a density ρa = 3.5 × 103 kg/m3 and median size of 100 nm. The shear rate
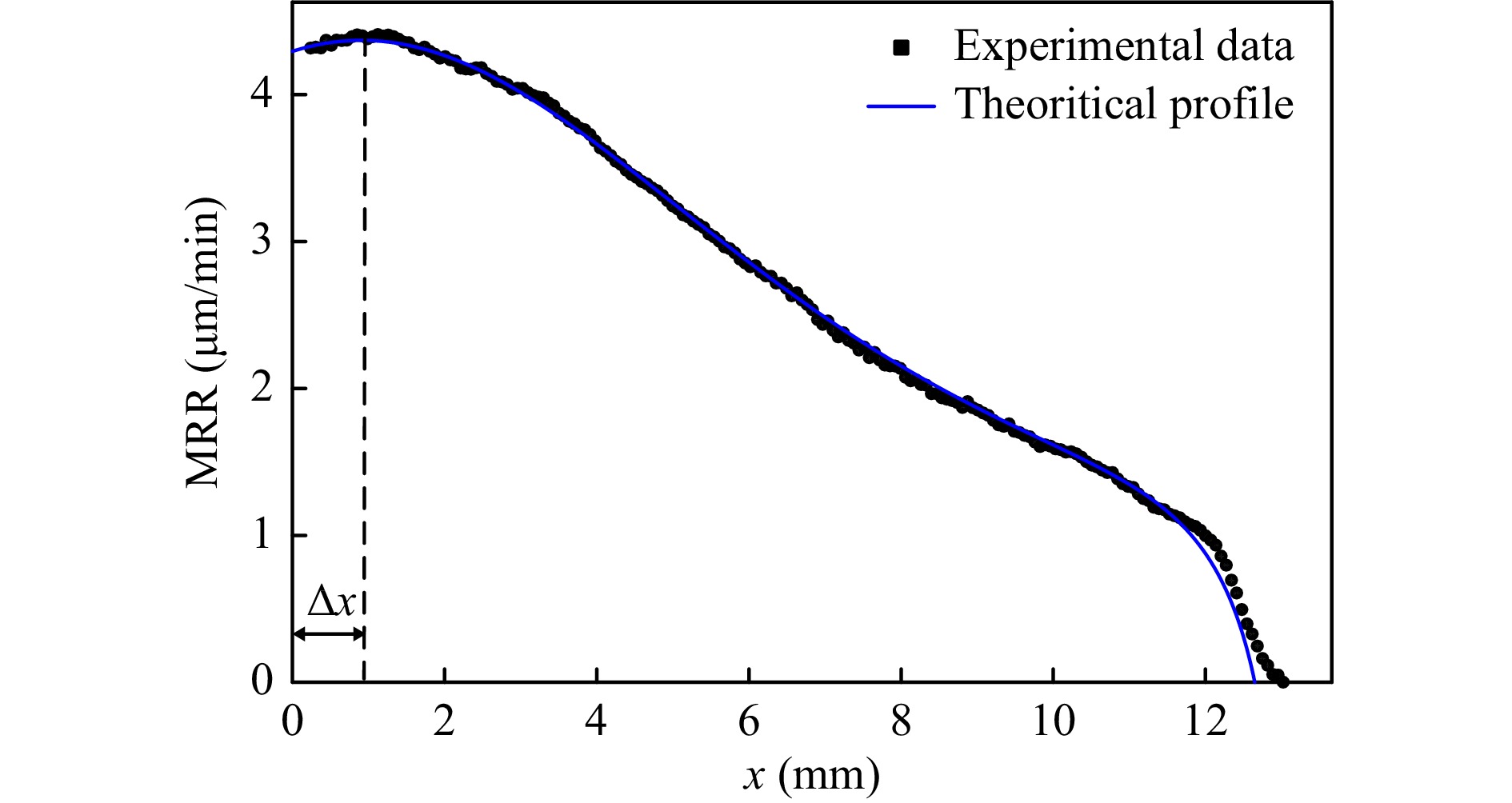
$\mathop \gamma \limits^ \bullet $ exceeds 500/s in the steady shearing state during the polishing process with the typical process parameters, according to the contact model of the MRF proposed in this study. Therefore, we adopted$\mathop \gamma \limits^ \bullet $ = 1000/s and relaxation time tr = 10−3 s. Thus, we can obtain the theoretical material removal rate along the long axis of the removal function based on the friction fitting results of pressure and friction under typical process parameters. The actual and theoretical material removal profiles along the long axis of the removal function are shown in Fig. 9, and the coefficient, CMRF is approximately 0.12. The results demonstrate that the material removal model proposed in this study can depict the material removal distribution along the long axis of the MRF removal function. Moreover, the material removal model proposed here can also illustrate the deviation between the projection point of the lowest point of polishing wheel and the highest material removal of the removal function, which is also shown in Fig. 10. The deviation Δx along the long axis of the removal function is determined by the MR polishing fluid properties and process parameters. To achieve a highly determined fabrication of workpieces, this deviation should be considered in the actual polishing process. -
Magnetorheological finishing (MRF) is a typical multi-disciplinary processing technology, an accurate theoretical model of removal function with decoupled parameters has not been established so far. Through the research of the rheological characteristics of MR polishing fluid and the contact model of MRF process, a new mechanism to reveal the source of shear force in MRF is proposed based on the granular flow theory and a novel material removal model is established.
The established model is also based on the shear stress in the polishing process similarly to the previous studies. However, it is different from simplifying the MR polishing fluid as Newtonian fluid and calculating the shear stress based on hydrodynamics directly. The MR fluid shear modulus and storage modulus under dynamic oscillation mode are analyzed in this work. Then, the MR polishing fluid in the polishing area is divided into two layers according to the actual contact model of MRF. The upper layer is a magnetized solid-like body, whereas the lower layer is a sheared thinning dense granular flow that consists of particles and base liquid added in the fluid. The shear force generation mechanism of MRF is investigated based on the granular flow theory and the material removal model is established based on the contact model of MRF. The comparison of the theoretical and actual polishing removal function profiles along the long axis indicates that the proposed material removal model in this study can accurately describe the actual material removal along the long axis of the MRF removal function.
The model covers the main parameters that influence the material removal rate and removal function distribution. Such parameters include magnetic field characteristics, shear rate (polishing wheel rotation speed), MR fluid viscosity and the size of added particles, removal function area, polishing wheel sizeparameters that influence the material removal function are as follows:
$$\begin{split} MRR(x) =& {C_{MRF}}\frac{{1 - exp\left[ - {m_a}{g_a}\left({h_1} - {h_0} - \dfrac{{{x^2}}}{{2R}}\right){{\left(\dfrac{{2\eta {t_r}}}{{3n}}{{\mathop \gamma \limits^ \bullet }^2}\right)}^{ - 1}}\right]}}{{1 - exp\left[ - {m_a}{g_a}\left(R + {h_0} + \dfrac{{{x^2}}}{{2R}}\right){{\left(\dfrac{{2\eta {t_r}}}{{3n}}{{\mathop \gamma \limits^ \bullet }^2}\right)}^{ - 1}}\right]}}\\&{\left(\frac{{{a^2}}}{{4b}}(b - x)\right)^{ - \frac{1}{2}}}\left({\mu _0}{F_N} + \beta \frac{{\mathop \gamma \limits^ \bullet \overline d }}{{\sqrt {k\overline {{\rho _s}} } }}{F_N}^{0.5}\right)\end{split} $$ (9) (a) The size of particles added in MR polishing fluid mainly affects the inertia parameter of the sheared granular flow, and then affects the shear force over the workpiece and the material removal rate.
(b) The magnetic field strength in the polishing area and the rotating speed of polishing wheel will determine the concentration of abrasives in the sheared granular flow and the shear force over the workpiece, then the material removal rate and the distribution of removal function will be affected.
(c) The working gap has the opposite effect on the positive pressure on the workpiece and the surface effective friction coefficient. However, the shear force will still decrease as working gap increases under the conventional processing parameters and typical MR polishing fluid composition, which is also proved by large numbers of experiments.
In general, the effects of polishing parameters on material removal rate and removal function distribution can be evaluated with the novel material removal model proposed in this work. This is very importance for the research of MRF technology. However, it is necessary to adjust the variables of the model according to the processing parameters and polished materials to improve the prediction accuracy. This is also the deficiency of the material removal model and one of the subsequent research contents.
Therefore, the main conclusions are as follows:
(1) In the MRF process, there exists the partial solid-liquid conversion of MR polishing fluid near the workpiece surface, and a sheared dense granular flow is formed between the solid-like magnetized core and the workpiece.
(2) The shear stress generation mechanism of MRF process can be investigated based on granular flow theory and the contact model of MRF.
(3) The material removal model proposed based on dense granular theory can decouple the main parameters that affect the material removal of MRF.
(4) The peak point of MRF removal function is not coincident with the maximum pressure point. It is the result of the combined effect of abrasives concentration over contact area and shear force distribution. This is particularly important for the position calibration and the control of removal function stability during actual polishing process.
The results of this study provide theoretical support for research on the mechanism and optimization of the MRF technology. The material removal model proposed in this paper is beneficial for the researchers to improve the MR polishing fluid composition and processing parameters according to the polishing requirements. Moreover, the studies of the material removal prediction and removal function distribution changes under different polishing conditions can also be targeted with the theoretical model. The proposed material removal model in this work overcomes the limitations of the traditional Preston equation to describe the material removal of MRF and will be promising for the mechanism studies and process improvement of other optical fabrication technologies.
-
Y. Bai and X. J. Zhang acknowledge the funding provided by the National Natural Science Foundation of China (Nos. 62127901, 6207031149 and11903035).
Material removal model of magnetorheological finishing based on dense granular flow theory
- Light: Advanced Manufacturing 3, Article number: (2022)
- Received: 24 February 2022
- Revised: 24 June 2022
- Accepted: 24 June 2022 Published online: 06 July 2022
doi: https://doi.org/10.37188/lam.2022.041
Abstract: Magnetorheological finishing (MRF) technology is widely used in the fabrication of high-precision optical elements. The material removal mechanism of MRF has not been fully understood because MRF technology involves the integration of electromagnetics, contact mechanics, and materials science. In this study, the rheological properties of the MR polishing fluid in oscillation model have been investigated. We propose that the shear-thinned MR polishing fluid over the polishing area should be considered a dense granular flow, based on which a new contact model of MRF over the polishing area has been constructed. Removal function and processing force test experiments were conducted under different working gaps. The normal pressure and effective friction equations over the polishing area were built based on the continuous medium and dense granular flow theories. Then, a novel MRF material removal model was established. A comparison of the results of the theoretical model with actual polishing results demonstrated the accuracy of the established model. The novel model proposed herein reveals the generation mechanism of shear force over a polished workpiece and realizes effective decoupling of the main processing parameters that influence the material removal of MRF. The results of this study will provide new and effective theoretical guidance for the process optimization and technology improvement of MRF.
Research Summary
Material removal model of magnetorheological finishing based on dense granular flow theory
As an ultra-high precision polishing technology, magnetorheological finishing (MRF) possesses many advantages and broad application prospects. However, MRF is a typical multi-disciplinary processing technology, and its material removal mechanism is extremely complex. Yang Bai and his colleagues from Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, revealed the mechanism of shear force generation mechanism in MRF process based on particle flow theory by investigate the rheological properties of MR polishing fluid in the polishing process. A novel material removal model of MRF with decoupled parameters is established and verified by experiments. The established material removal model has a good guiding role for the improvement of MRF technology and the expansion of application fields.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article′s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article′s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.



















 DownLoad:
DownLoad: